Простейшие квадратурные формулы

Формулы прямоугольников.Как известно, определенный интеграл в силу своего построения есть предел интегральных сумм:

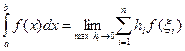, (5.27)

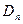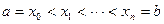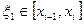каждая, из которых соответствует некоторому разбиению : отрезка и произвольному набору точек для каждого разбиения; .

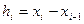Ограничиваясь конечным числом слагаемых в правой части равенства (5.27) и принимая в качестве набора 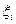те или иные значения аргумента из отрезков 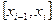, можно получить различные формы приближенного интегрирования. Так, принимая в качестве набора 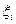значения левых или правых концов отрезков 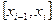, получим соответственно формулу левых или правых прямоугольников :

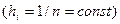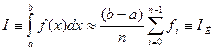, (5.28)

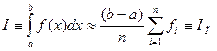. (5.29)

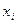Название этих формул связано с их геометрической интерпретацией. Если в плоскости Х0У (рис 5.1) построить кривую y = f(x), разбить отрезок на n частей точками сетки 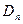, то формула левых прямоугольников в качестве приближенного значения интеграла даст суммарную площадь штрихованных прямоугольников (рис. 5.1, а); а формула правых прямоугольников - суммарную площадь штрихованных прямоугольников (рис. 5.1, б).

Пример 5.3. с помощью формул левых и правых прямоугольников вычислить 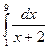, полагая n = 4.

Зная приделы интегрирования a = 1 и b = 9, находим шаг 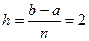; тогда точками разбиения служат 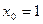, , 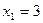, , 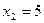, 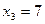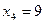а значения подынтегральной функции 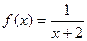в этих точках таковы:

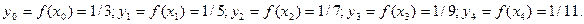
Далее найдем числовое значение интеграла, пользуясь формулой (5.28):

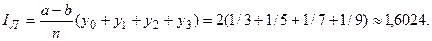
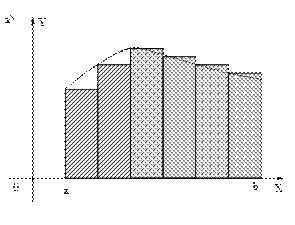
Рисунок 5.1 – Графическая интерпретация формулы прямоугольников:
а) левых прямоугольников, б) правых прямоугольников, в) центральных
прямоугольников.

Если вычисление определенного интеграла произвести по формуле (5.29), то получим:

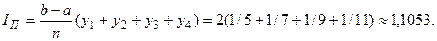
Наиболее часто используемой формулой, основанной на идее представления определенного интеграла в виде интегральной суммы, является формула прямоугольников, где в качестве 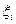берут середины отрезков 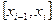. Для равномерной сетки 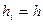эта формула имеет следующий вид:

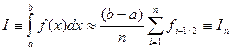, (5.30)

где ; ; .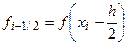

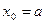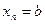Найдем выражение для остаточного члена приближенной формулы (5.30) с этой целью представим интеграл, входящий в левую часть соотношения (4.30), в виде суммы:

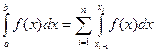. (5.31)

Предполагая, что функция f(x) дважды дифференцируема, т.е. 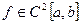, запишем для функции f(x) на каждом из отрезков 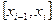формулу Тейлора остаточным членом в форме Лагранжа:

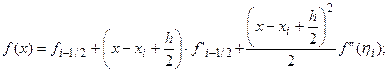
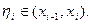(5.32)

Подставим в правую часть соотношения (5.31) вместо функции f ее представление (5.32) и выполним интегрирование, используя вторую теорему о среднем значении функции:

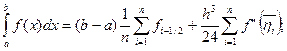
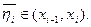
В силу непрерывности второй производной существует такая точка 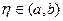, что

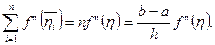
Используя это соотношение, окончательно имеем

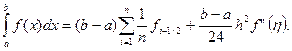(5.33)

Сравнивая формулы (5.30) и (5.33), получаем выражение для остаточного члена квадратурной формулы (5.30):

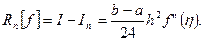(5.34)

Таким образом, оценку погрешности квадратурной формулы (5.30) можно представить в следующем виде:

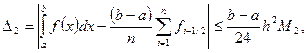(5.35)

где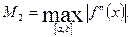

Полученные выражение для остаточного члена (5.34) и погрешности (5.35) показывают, что формула (5.30) является точной для любой линейной функции, поскольку вторая производная такой функции равна нулю, а, следовательно, остаточный член и погрешность также равны нулю.

Перейдем к оценке погрешности приближенного значения 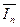. Если значения функции, используемые в квадратичной формуле, получены, приближено или вычисления не могут быть выполнены абсолютно точно, то это влечет за собой появление вычислительной погрешности и погрешностей округления. Пусть значения 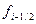в формуле (5.30) получены с одинаковой абсолютной погрешностью 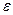; тогда суммарная вычислительная погрешность 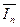составит

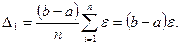(5.36)

Эта погрешность не зависит от числа разбиений отрезка интегрирования, а пропорциональна только его длине.

Пример 5.4. Вычислить с помощью формулы прямоугольников интеграл 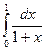, полагая n = 4. Оценить погрешность полученного приближенного значения.

По заданным пределам интегрирования и числу разбиений n определим шаг:

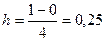. далее на основании формулы (5.30) имеем

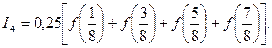
Вычислив необходимые значения функции с тремя верными в узком смысле знаками 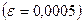, получим

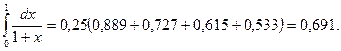
Погрешность метода оценим по формуле (5.35), для чего предварительно найдем максимум абсолютной величины второй производной подынтегральной функции:

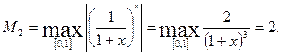
Таким образом, погрешность метода есть

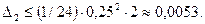
Пользуясь формулой (5.36), найдем погрешность входных данных:

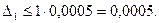
Следовательно, за полную погрешность приближенного вычисления интеграла можно принять 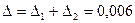, а окончательный ответ записать в виде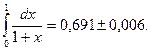

Формула трапеций.Перейдем теперь к другому способу построения квадратурных формул, связанному с аппроксимацией подынтегральной функции интерполяционным многочленом. Рассмотрим простейший случай аппроксимации многочленом первой степени с узлами в точках a и b:

; .

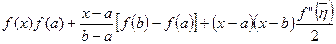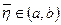Интегрируя правую и левую части этого равенства и используя вторую теорему о среднем значении функции при интегрировании последнего слагаемого правой части, находим:

; .

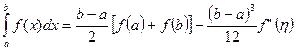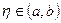Таким образом, предполагая, что отрезок интегрирования мал, получаем квадратурную формулу, называемую формулой трапеций:

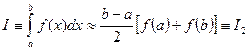(5.37)

с остаточным членом

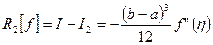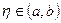; . (5.38)

Используя выражение (5.35) для остаточного члена, опенку погрешности квадратурной формулы (5.37) можно представить в виде

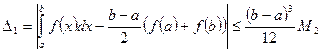, (5.39)

где .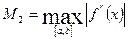

Полученные выражения для остаточного члена (5.38) и погрешности (5.39) показывают, что квадратурная формула (5.37) является точной для всех линейных функций, поскольку вторая производная таких функций равна нулю, а, следовательно, равны пулю остаточный член и погрешность.

Пример 5.5. Вычислить с помощью формулы трапеций интеграл 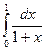. Оценить погрешность полученною приближенного значения.

На основании формулы (5.37) имеем

.

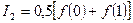Вычислив необходимые значения функции, получим

.

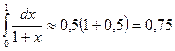Погрешность метода оценим по формуле (5.39), используя значение М=2 полученное в примере 5.4:

.

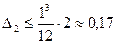Вычислительная погрешность, очевидно, равна нулю, так как значе­ния функции и 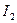, найдены абсолютно точно.

Итак, окончательно имеем .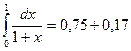

Отметим, что в примере 5.5 получилось гораздо менее точное решение, чем в примере 5.4. Однако использование в примере 5.5 формулы трапеций имеет свои преимущества. Во-первых, если подынтегральная функция задана в виде таблицы ее значений в узлах 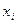, то для использования формулы прямоугольников необходимо определить значения этой функции еще и в точках 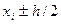, что вносит дополнительные трудности и дополнительную погрешность. Во-вторых, в примере 5.5 значения подынтегральной функции были вычислены всего лишь в двух точках, в то время как в примере 5.4 - в четырех точках, что, естественно, потребовало большего времени.

Приведенные рассуждения показывают, что ценность квадратурной формулы определяется не только формой ее остаточного члена (или погрешности), но и другими факторами, например временем счета.