Экстраполяционный метод Адамса
При решении дифференциального уравнения методом Рунге-Кутта необходимо производить много вычислений для нахождения каждого 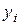 . В том случае, когда правая часть уравнения сложное аналитическое выражение, решение такого уравнения методом Рунге-Кутта вызывает большие трудности. Поэтому на практике применяется метод Адамса, который не требует многократного подсчета правой части уравнения.
. В том случае, когда правая часть уравнения сложное аналитическое выражение, решение такого уравнения методом Рунге-Кутта вызывает большие трудности. Поэтому на практике применяется метод Адамса, который не требует многократного подсчета правой части уравнения.
Пусть дано дифференциальное уравнение
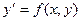 , (5.89)
, (5.89)
с начальным условием
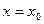 ,
, 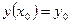 . (5.90)
. (5.90)
Требуемся найти решение этого уравнения на отрезке [a.b].
Разобьем отрезок [a,b] на n равных частей точками 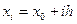
(i = 1, 2,..., n), a 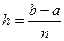 – проинтегрируем дифференциальное уравнение). Выберем участок
– проинтегрируем дифференциальное уравнение). Выберем участок 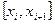 и проинтегрируем дифференциальное уравнение (5.89); тогда получим
и проинтегрируем дифференциальное уравнение (5.89); тогда получим
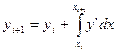 ,
,
или
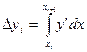 . (5.91)
. (5.91)
Для нахождения производной воспользуемся второй интерполяционной формулой Ньютона (ограничиваясь при этом разностями третьего порядка):
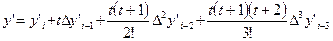 . (5.92)
. (5.92)
или
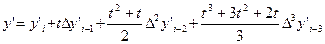 . (5.93)
. (5.93)
Подставляя выражение для 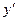 из формулы (5.93) в соотношение (5.91) и учитывая, что
из формулы (5.93) в соотношение (5.91) и учитывая, что 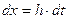 , имеем
, имеем
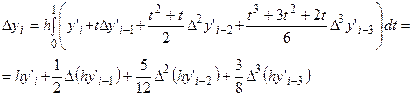 (5.94)
(5.94)
Обозначим в дальнейшем 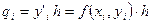 (i = 0,1,2,…,n).
(i = 0,1,2,…,n).
Тогда для любой разности имеем 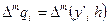 и
и
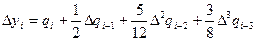 . (5.95)
. (5.95)
По формуле 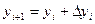 получаем решение уравнения. Формула (5.95) носит название экстраполяционной формулы Адамса.
получаем решение уравнения. Формула (5.95) носит название экстраполяционной формулы Адамса.
Для начала процесса нужны четыре начальных значения 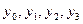 - так называемый начальный отрезок, который может быть найден, исходя из начального условия (5.90) с использованием одного из известных методов. Обычно начальный отрезок решения находится методом Рунге-Кутта.
- так называемый начальный отрезок, который может быть найден, исходя из начального условия (5.90) с использованием одного из известных методов. Обычно начальный отрезок решения находится методом Рунге-Кутта.
Зная 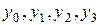 можно определить
можно определить
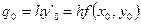 ;
; 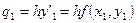 ;
;
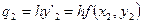 ;
; 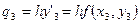 . (5.96)
. (5.96)
Далее составляется таблица разностей величины q (табл. 7).
Таблица 7. Таблица разностей величины q
| I | 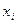
| 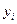
| 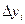
| 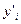
| 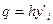
| 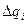
| 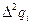
| 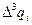
|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |

| 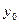
| - | 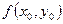
| 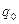
| 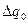
| 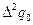
| 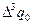
| |
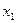
| 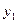
| - | 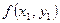
| 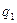
| 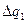
| 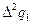
| - | |
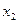
| 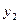
| - | 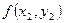
| 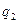
| 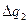
| - | - | |
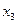
| 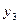
| 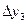
| 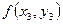
| 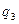
| - | - | - | |
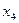
| 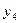
| - | - | - | - | - | - | |
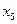
| - | - | - | - | - | - | - | |
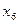
| - | - | - | - | - | - | - |
Метод Адамса заключается в продолжении диагональной таблицы разностей с помощью формулы (5.95). Используя числа 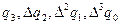 , которые располагаются в таблице по диагонали, пологая в формуле (5.95)
, которые располагаются в таблице по диагонали, пологая в формуле (5.95)
n = 3 (известное последнее значение у есть 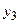 ), получаем:
), получаем:
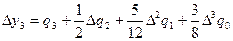 .
.
Полученное значение 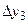 вносят и таблицу и находят
вносят и таблицу и находят 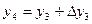 . Затем используя значения
. Затем используя значения 
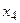 и
и 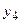 находят
находят 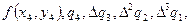 т.е. получается новая диагональ. По этим данным вычисляют
т.е. получается новая диагональ. По этим данным вычисляют
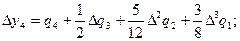
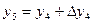 .
.
Таким образом, продолжают таблицу решения, вычисляя правую часть дифференциального уравнения (5.89) на каждом этапе только один раз.
Для грубой оценки погрешности применяют принцип Рунге, который состоит в следующем:
1. Находят решение дифференциального уравнения при шаге h.
2. Значение шага удваивают и находят решение при шаге Н = 2h.
3. Вычисляют погрешность метода по формуле
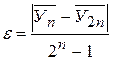 , (5.97)
, (5.97)
где 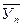 - значение приближенного вычисления при двойном шаге H=2h;
- значение приближенного вычисления при двойном шаге H=2h; 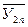 - значение приближенного вычисления при шаге h.
- значение приближенного вычисления при шаге h.
Метод Адамса применяется также и для решения систем дифференциальных уравнений и дифференциальных уравнений n-гo порядка.
Пусть задана система двух уравнений
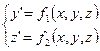 (5.98)
(5.98)
Тогда экстраполяционные формулы Адамса для этой системы имеют вид
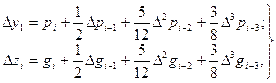 (5.99)
(5.99)
где 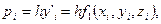
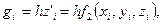 и
и 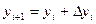 ,
,
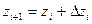 .
.
Дата добавления: 2015-11-06; просмотров: 3584;
