Квадратурные формулы Ньютона – Котеса.
Рассмотрим формулы численного интегрирования, имеющие более сложную структуру. Описанные выше методы численного интегрирования являлись интерполяционными, включая в определенном смысле и формулы прямоугольников. Это означает, что подынтегральная функция аппроксимировалась интерполяционным многочленом. Если интегрируемая функция достаточно гладкая, а отрезок интегрирования конечен, то можно получить достаточно хорошие результаты. С другой стороны, трудно рассчитывать на хорошую аппроксимацию интегрируемой функции многочленом, если сама функция или ее производные невысоких порядков имеют особенности. В таких случаях подынтегральную функцию целесообразно представить в виде произведения двух сомножителей: 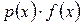 , которые должны обладать следующими тремя свойствами. Во-первых, весовой множитель р(х) должен отражать все особенности интегрируемой функции. Во-вторых, моменты
, которые должны обладать следующими тремя свойствами. Во-первых, весовой множитель р(х) должен отражать все особенности интегрируемой функции. Во-вторых, моменты
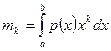 (k = 0,1,…),
(k = 0,1,…),
где [а, b] - отрезок интегрирования, должны вычисляться аналитически.
В-третьих, погрешность аппроксимации функции f(x) многочленом должна быть мала.
Перейдем теперь к построению самих квадратурных формул. Будем их строить в том же виде, что и раньше:
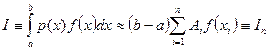 . (5.41)
. (5.41)
В общем случае, как уже отмечалось, формула (5.41) имеет 2n свободных параметров - это узлы квадратуры 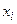 и весовые множители
и весовые множители 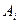 . Число n будем предполагать фиксированным. Выбор свободных параметров определяется теми требованиями, которые предъявляются к квадратурной формуле условиями практической задачи. Такими требованиями могут быть, например, максимально возможная точность, минимальная вычислительная погрешность, фиксирование некоторых (а возможно, и всех) весовых множителей или узлов квадратуры.
. Число n будем предполагать фиксированным. Выбор свободных параметров определяется теми требованиями, которые предъявляются к квадратурной формуле условиями практической задачи. Такими требованиями могут быть, например, максимально возможная точность, минимальная вычислительная погрешность, фиксирование некоторых (а возможно, и всех) весовых множителей или узлов квадратуры.
Начнем с относительно простого случая, когда узлы определены заранее, и можно варьировать лишь выбором весовых множителей 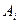 . Идея интерполяционных квадратур заключается в следующем. Аппроксимируем функцию f интерполяционным многочленом в форме Лагранжа степени n-1 по n различным узлам
. Идея интерполяционных квадратур заключается в следующем. Аппроксимируем функцию f интерполяционным многочленом в форме Лагранжа степени n-1 по n различным узлам 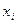 :
:
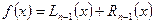 .
.
Проинтегрируем правую и левую части этого равенства на отрезке [а,b], предварительно умножив их на весовую функцию р(х):
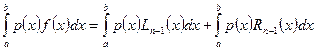 . (5.42)
. (5.42)
Преобразуем первое слагаемое правой части этого соотношения.
Для этого подставим вместо 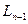 его явное выражение и поменяем местами операции интегрирования и суммирования:
его явное выражение и поменяем местами операции интегрирования и суммирования:
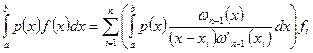 . (5.43)
. (5.43)
Здесь 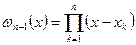 . Первый из множителей, входящих под знак суммы, является числовым коэффициентом, пропорциональным длине отрезка интегрировании и зависящим только от расположения узлов и свойств функции р(х) (по не функции f).
. Первый из множителей, входящих под знак суммы, является числовым коэффициентом, пропорциональным длине отрезка интегрировании и зависящим только от расположения узлов и свойств функции р(х) (по не функции f).
Предполагая теперь, что второе слагаемое правой части соотношения (5.42) мало, получаем приближенную квадратурную формулу (5.41) с заданными узлами 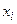 и коэффициентами
и коэффициентами 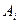 , определяемыми следующим образом:
, определяемыми следующим образом:
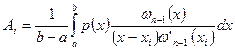 (i = 1,2,…,n). (5.44)
(i = 1,2,…,n). (5.44)
Построенная таким образом квадратурная формула называется интерполяционной.
Перейдем к оценке погрешности формулы (5.41) с коэффициентами (5.44). Для этого проинтегрируем остаточный член интерполяционной формулы:
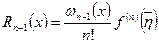 .
.
Подставляя приведенное выражение во второе слагаемое равенства (5.42), получаем
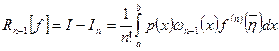 ;
; 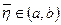 .
.
Если функция f имеет на отрезке итерирования непрерывную производную порядка n, а произведение 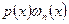 сохраняет на том же отрезке свой знак, то дли остаточного члена можно получить следующее выражение:
сохраняет на том же отрезке свой знак, то дли остаточного члена можно получить следующее выражение:
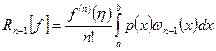 ;
; 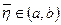 . (5.45)
. (5.45)
и, следовательно, оценка погрешности квадратуры принимает вид
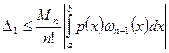 , (5.46)
, (5.46)
где 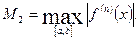 Полученная оценка при указанных выше условиях является не улучшаемой.
Полученная оценка при указанных выше условиях является не улучшаемой.
Если же произведение 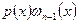 не сохраняет знак па отрезке интегрирования, но в этом случае получается лишь грубая оценка погрешности:
не сохраняет знак па отрезке интегрирования, но в этом случае получается лишь грубая оценка погрешности:
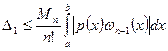 ,
,
которая может оказаться далеко не оптимальной. Полому в подобных случаях пользуются другими соображениями при построении явного выражения для остаточного члена и погрешности.
Пример 5.6. Построить квадратурную формулу (5.41) дли отрезка [-1,1] с узлами 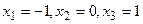 и весовой функцией
и весовой функцией 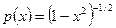 .
.
По существу, необходимо определить коэффициенты Ai, (i = 1,2,3) формулы (5.41). Используя выражение (5.44) для искомых коэффициентов, получаем
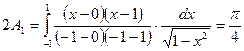 ,
,
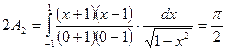 ,
,
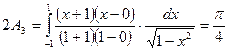 .
.
Таким образом, искомая формула имеет вид
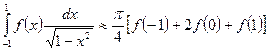 .
.
В практических расчетах особый интерес представляет случай, когда узлы квадратурной формулы задаются в виде равноотстоящих точек отрезка [а, b]: 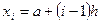 (i = 1,2,…,n), а весовая функция р(х) тождественно равна единице. При таких предположениях формулу (5.41) можно преобразовать к виду
(i = 1,2,…,n), а весовая функция р(х) тождественно равна единице. При таких предположениях формулу (5.41) можно преобразовать к виду
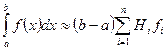 . (5.47)
. (5.47)
При различных n получаем квадратурные формулы Ньютона-Котеса. Коэффициенты 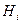 , называемые коэффициентами Котеса, определяются из соотношения (5.44):
, называемые коэффициентами Котеса, определяются из соотношения (5.44):
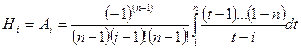 , (5.48)
, (5.48)
где n >1; i = 1,2,…,n; 0!=1.
Эти коэффициенты обладают следующими полезными при их вычислении свойствами.
1. Симметричные коэффициенты (первый и n-й, второй и (n-1)-й, ...) равны между собой:
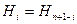 . (5.49)
. (5.49)
2. Сумма всех коэффициентов равна единице:
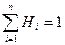 .
.
В табл. 6 приведены значения коэффициентов Котеса для
n = 2, 3, 4, 5, 6.
Таблица 6. Значения коэффициентов Котеса для n = 2, 3, 4, 5, 6
| n | i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | i = 6 |
| 1/2 | 1/2 | - | - | - | - | |
| 1/6 | 4/6 | 1/6 | - | - | - | |
| 1/8 | 3/8 | 3/8 | 1/8 | - | - | |
| 7/90 | 32/90 | 12/90 | 32/90 | 7/90 | - | |
| 19/288 | 75/288 | 50/288 | 50/288 | 75/288 | 19/288 |
Остановимся на частном случае квадратурной формулы (5.47), получающемся при n = 3. Применяя формулу (5.48), имеем
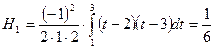 .
.
Далее, используя равенства (5.49), найдем
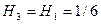 ,
, 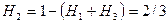 .
.
Таким образом, искомая квадратурная формула, называемая формулой Симпсона, имеет вид
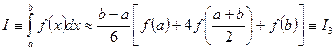 . (5.50)
. (5.50)
Формула (5.50) является точной для всех многочленов нулевой, первой, и второй степеней. Формула Симпсона обладает также так называемым свойством повышенной точности, которое заключается в том, что она является точной не только для многочленов второй степени, но и для многочленов третьей степени.
Оценка погрешности имеет вид
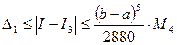 , (5.51)
, (5.51)
где 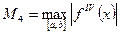 .
.
Пример 5.7. Вычислить с помощью формулы Симпсона интеграл 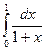 . Оценить погрешность полученного приближения.
. Оценить погрешность полученного приближения.
Вычислив необходимые значения подынтегральной функции в точках 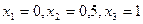 , подставим их в формулу (5.50):
, подставим их в формулу (5.50):
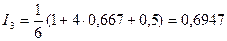 .
.
Учитывая, что 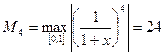 , и используя формулу (5.51), для метода получим погрешность
, и используя формулу (5.51), для метода получим погрешность 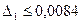 .
.
Найдем вычислительную погрешность
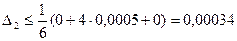 .
.
Складывая погрешности и округляя результат, окончательно имеем
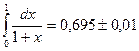 .
.
Дата добавления: 2015-11-06; просмотров: 3150;
