Формулы численного интегрирования

Пусть требуется вычислить интеграл

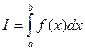(5.24)

Из курса математического анализа известно, что для непрерывной на отрезке [a,b] функции f интеграл (5.24) существует и равен разности значений для первообразной F для функции f в точках b и a:

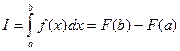. (5.25)

Однако в подавляющем большинстве практических задач первообразную F не удается выразить через элементарные функции. Кроме того, функция f часто задается в виде таблицы ее значений для определенных значений аргумента. Все это порождает потребность в приближенных методах вычислении интеграла (5.24), которые можно условно подразделить на аналитические и численные. Первые заключаются в приближенном построении первообразной и дальнейшем использовании формулы (5.25). Вторые позволяют непосредственно найти числовое значение интеграла, основываясь на известных значениях подынтегральной функции (а иногда и ее производной) в заданных точках, называемых узлами. В настоящей главе остановимся лишь на численных методах интегрирования функций. Сам процесс численного определения интеграла называется квадратурой, а соответствующие формулы – квадратурными.

В зависимости от способа задания подынтегральной функции будем рассматривать два различных в смысле их реализации случая численного интегрирования.

Задача 1. На отрезке [a,b] в узлах 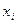заданы значения 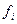некоторой функции f, принадлежащей определенному классу F. Тре6уется приближенно вычислить интеграл (5.24) и оценить погрешность полученного значения. Так обычно ставится задача численного интегрирования в том случае, когда подынтегральная функция задана в виде таблицы.

Задача 2. На отрезке [a,b] функция f(x) задана в виде аналитического выражения. Требуется вычислить интеграл (5.24) с заданной предельно допустимой погрешностью .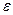

Один из способов решения сформулированных задач основан на использовании различных квадратурных формул вида

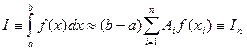(5.26)

С известным остаточным членом 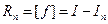или его оценкой.

В общем случае, как узловые точки 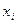, так и весовые множители (веса) 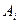заранее не известны и подлежат определению при выводе каждой конкретной квадратурной формулы на основе предъявляемых к ней требований.