Алгоритм решения задачи 2.

1. Представляют 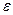в виде суммы трех неотрицательных слагаемых:

,

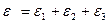где 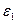- предельно допустимая погрешность вычисления 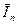; 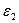- предельно допустимая погрешность метода; 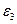- предельно допустимая погрешность округления результата.

2. Выбирают n в квадратурной формуле так, чтобы выполнялось неравенство

.

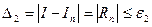3. Вычисляют 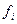с такой точностью, чтобы при подсчете 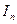по формуле (5.26) обеспечить выполнение неравенства

.

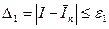Для этого, очевидно, достаточно вычислить все 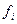с абсолютной погрешностью.

.

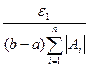4. Найденную в п. 3 величину 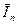округляют (если 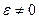) с предельно допустимой погрешностью 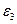до величины .

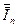5. Получают решение задачи в виде

.

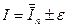Используемые в алгоритмах обеих задач квадратурные формулы строятся, как уже было сказано, на основании тех или иных критериев, определяющих положение узловых точек и величины весовых множителей. Такими критериями могут быть: представление интеграла в виде интегральной суммы; аппроксимация подынтегральной функции (например, многочленом) и последующее интегрирование аппроксимирующей функции; требование, чтобы формула (5.26) была абсолютно точной для определенного класса функций, и др.