Решение обыкновенных дифференциальных уравнений. Метод конечных разностей для численного решения дифференциальных уравнений
Метод последовательных приближений (метод Пикара)
Пусть дано уравнение
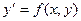 , (5.52)
, (5.52)
правая часть, которого в прямоугольнике 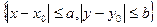 непрерывна и имеет непрерывную частную производную по у. Требуется найти решение уравнения (5.52), удовлетворяющее начальному условию
непрерывна и имеет непрерывную частную производную по у. Требуется найти решение уравнения (5.52), удовлетворяющее начальному условию
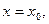
 . (5.53)
. (5.53)
Интегрируя обе части уравнения от  до
до 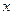 получим
получим

или
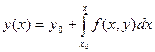 . (5.54)
. (5.54)
Уравнение (5.52) заменяется интегральным уравнением (5.54), в котором неизвестная функция у находится под знаком интеграла. Интегральное уравнение (5.54) удовлетворяет дифференциальному уравнению (5.52) и начальному условию (5.53). Действительно,
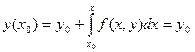 .
.
Заменяя в равенстве (5.54) функцию у значением 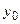 , получим первое приближение
, получим первое приближение
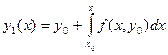 .
.
Затем в уравнении (5.54) заменив у найденным значением 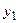 , получаем второе приближение:
, получаем второе приближение:
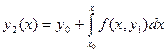 .
.
Продолжая процесс далее, последовательно находим
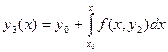 ,
,
…
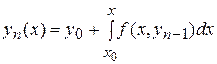 .
.
Таким образом, составляем последовательность функций
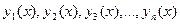 .
.
Справедлива следующая теорема.
Теорема 6.1. Пусть в окрестности точки 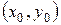 функция f(х,у) непрерывна и имеет ограниченную частную производную
функция f(х,у) непрерывна и имеет ограниченную частную производную 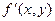 . Тогда в некотором интервале, содержащем точку
. Тогда в некотором интервале, содержащем точку 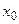 , последовательность
, последовательность 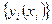 сходится к функции у(х), служащей решением дифференциального уравнения у = f(x,y) и удовлетворяющей условию
сходится к функции у(х), служащей решением дифференциального уравнения у = f(x,y) и удовлетворяющей условию
у(х0) = у0.
Оценка погрешности метода Пикара определяется, но формуле
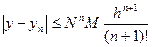 ,
,
где 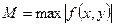 при
при 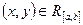 ;
; 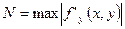 - постоянная Липшица для области
- постоянная Липшица для области 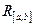 ;
; 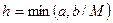 - величина определения окрестности
- величина определения окрестности 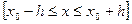 ; a и b – границы области R.
; a и b – границы области R.
Пример 1. Найти решение задачи Коши методом Пикара:

Найдём несколько приближений по методу Пикара. Пусть 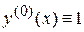 , тогда:
, тогда:
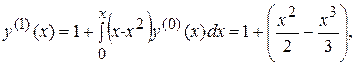
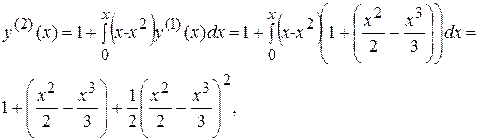
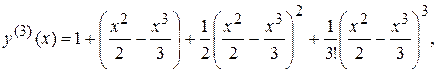
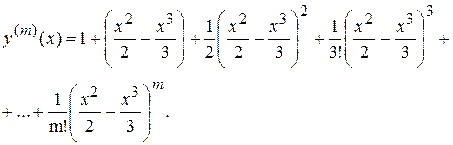
Как легко видеть
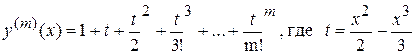 ,
,
то есть при 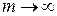 получим разложение в ряд функции
получим разложение в ряд функции  или
или 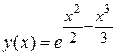 , что является аналитическим решением задачи.
, что является аналитическим решением задачи.
Метод последовательного дифференцирования. Пусть дано дифференциальное уравнение n-го порядка:
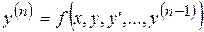 (5.55)
(5.55)
с начальными условиями
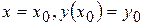 . (5.56)
. (5.56)
Представим решение 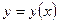 уравнения (5.55) в окрестностях точки х0 в виде ряда Тейлора:
уравнения (5.55) в окрестностях точки х0 в виде ряда Тейлора:
 (5.57)
(5.57)
где 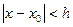 , а h – достаточно малая величина.
, а h – достаточно малая величина.
Для нахождения коэффициентов ряда (5.57) уравнение (5.55) дифференцируют по х нужное число раз, используя условия (5.56):
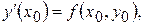
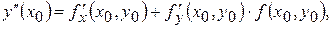
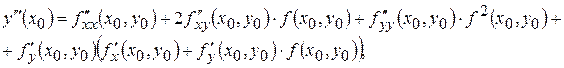
Если 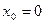 , то получается ряд Тейлора по степеням х:
, то получается ряд Тейлора по степеням х:
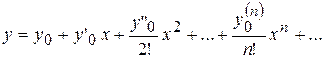 (5.58)
(5.58)
Этот метод редко применяется на практике, поскольку при достаточно большом n он слишком громоздок, а кроме того, при достаточном удалении х от х0 остаточный член может не стремиться к нулю.
Пример 2. Найти решение задачи Коши методом последовательного дифференцирования:

Решение
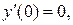


Тогда, подставив полученные значения в (5.58), получим ответ:
 .
.
Метод неопределенных коэффициентов. Пусть дано дифференциальное уравнение
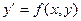 , (5.59)
, (5.59)
с начальным условием  .
.
Метод неопределенных коэффициентов состоит в том, что решение уравнения (5.59) отыскивают в виде ряда с неизвестными коэффициентами
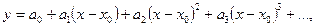 (5.60)
(5.60)
которые находят с помощью подстановки ряда (5.60) в уравнение (5.59), зачем приравнивают коэффициенты при одинаковых степенях х и используют начальное условие. Найденные значения коэффициентов 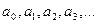 подставляют в ряд (5.59).
подставляют в ряд (5.59).
Пример 3. Найти решение дифференциального уравнения у" + ху = 0 такое, что у = 0 и y' = 1 при х = 0. Из теории дифференциальных уравнений следует, что такое решение существует и имеет вид степенного ряда
у = х + c2x2 + c3x3 + c4x4 + c5x5 + ….
Подставляя это выражение вместо у в правую часть уравнения, а вместо y" — выражение
2c2 + 3·2с3х + 4·3с4х2 + 5·4с5х3 + …,
затем, умножая на х и соединяя члены с одинаковыми степенями х, получим:
2c2 + 3·2c3x + (1 + 4·3c4) x2 + (c2 + 5·4c5) x3 + … = 0,
откуда при определении неизвестных коэффициентов получается бесконечная система уравнений: 2c2 = 0; 3·2с3 = 0; 1 + 4·3c4 = 0; c2 + 5·4c5 = 0;...
Решая последовательно эти уравнения,
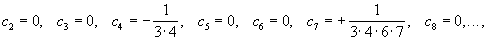
т. е.

Метод Эйлера
Решить дифференциальное уравнение 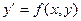 численным методом - это значит для заданной последовательности аргументов
численным методом - это значит для заданной последовательности аргументов 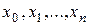 и числа
и числа  , не определяя функцию у = F(x), найти такие значения
, не определяя функцию у = F(x), найти такие значения 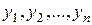 что
что 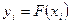 (i = 1,2,...,n) и
(i = 1,2,...,n) и 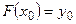 .
.
Таким образом, численные методы позволяют вместо нахождения функции у = F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина  называется шагом интегрирования. Рассмотрим некоторые из численных методов.
называется шагом интегрирования. Рассмотрим некоторые из численных методов.
Метод Эйлера является сравнительно грубым и применяется в основном для ориентировочных расчетов.
Пусть дано дифференциальное уравнение первого порядка
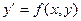 , (5.61)
, (5.61)
с начальным условием
 . (5.62)
. (5.62)
Требуется найти решение уравнения (5.61) на отрезке [а, b].
Разобьем отрезок [а,b] на n равных частей и получим последовательность 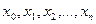 , где
, где 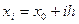 (i = 1, 2,..., n), a
(i = 1, 2,..., n), a 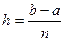 - шаг интегрирования.
- шаг интегрирования.
Выберем k-й участок 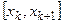 и проинтегрируем уравнение (5.61):
и проинтегрируем уравнение (5.61):
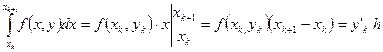 . (5.63)
. (5.63)
Тогда формула (5.63) примет вид
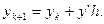 (5.64)
(5.64)
Обозначив, 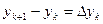 т.е.
т.е. 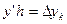 , получим
, получим
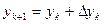 (5.65)
(5.65)
Продолжая этот процесс и каждый раз принимая подынтегральную функцию на соответствующем участке постоянной и равной ее значению в начале участка, получим таблицу решений дифференциального уравнения на заданном отрезке [а, b].
Если функция f(x,y) в некотором прямоугольнике
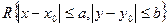
удовлетворяет условию
 (N = const) (5.66)
(N = const) (5.66)
и, кроме того.
 (М = const) (5.67)
(М = const) (5.67)
то имеет место следующая оценка погрешности:
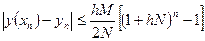 , (5.68)
, (5.68)
где 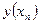 - значение точного решения уравнения (5.61) при
- значение точного решения уравнения (5.61) при 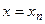 ,а
,а 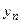 - приближенное значение, полученное на n-м шаге.
- приближенное значение, полученное на n-м шаге.
Формула (5.68) имеет в основном теоретическое применение. На практике, как правило, применяют "двойной просчет". Сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагом  . Погрешность более точного значения
. Погрешность более точного значения  оценивается формулой
оценивается формулой
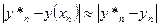 (5.69)
(5.69)
Пример:

Решение:
Разобьём отрезок на n частей (n=4): 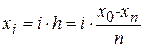 , i=1,…,n-1
, i=1,…,n-1
h=0,25
| x0 | x1 | x2 | x3 | x4 | |
| x | 0,25 | 0,5 | 0,75 |
Далее по формуле (5.56) получим текущие значения yi:
| x | 0,25 | 0,5 | 0,75 | ||
| y | 67/64 (1,05) | 1139/1024 (1,11) | 76313/ 65536 (1,16) | ||
| f(x,y) | 3/16 (0,19) | 67/256 (0,26) | 3417/16386 (0,21) |
| X | Y(x) | Ряд | Эйлера |
| 0,25 | 1,026384 | 1,026042 | |
| 0,5 | 1,086904 | 1,083333 | 1,046875 |
| 0,75 | 1,150993 | 1,140625 | 1,112305 |
| 1,18136 | 1,166667 | 1,164444 |
Метод Эйлера может быть применен к решению систем дифференциальных уравнений и дифференциальных уравнений высших порядков. Однако в последнем случае дифференциальные уравнения должны быть приведены к системе дифференциальных уравнений первого порядка.
Пусть задана система двух уравнений первого порядка
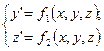 (5.70)
(5.70)
с начальными условиями
 ,
,  (5.71)
(5.71)
Приближенные значения 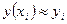 и
и 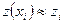 находятся по формулам
находятся по формулам
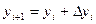 ,
, 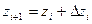 (5.72)
(5.72)
где 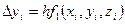 ,
, 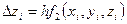 (i = 0,1,2,…). (5.73)
(i = 0,1,2,…). (5.73)
Метод Рунге-Кутта
Метод Рунге-Кутта является одним из методов повышенной точности. Он имеет много общего с методом Эйлера.
Пусть на отрезке [а, b] требуется найти численное решение уравнения
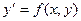 , (5.74)
, (5.74)
с начальным условием
 .(5.75)
.(5.75)
Разобьем отрезок [а, b] на n равных частей точками 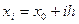
(i = 1,2,..., n, a 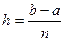 - шаг интегрирования). В методе Рунге-Кутта, так же, как и в методе Эйлера, последовательные значения у, искомой функции у определяются по формуле
- шаг интегрирования). В методе Рунге-Кутта, так же, как и в методе Эйлера, последовательные значения у, искомой функции у определяются по формуле
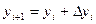 . (5.76)
. (5.76)
Если разложить функцию у в ряд Тейлора и ограничиться членами до 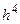 включительно, то приращение функции
включительно, то приращение функции  можно представить в виде
можно представить в виде
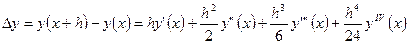 , (5.77)
, (5.77)
где производные 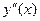 ,
,  ,
, 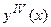 находят последовательным дифференцированием из уравнения (5.74).
находят последовательным дифференцированием из уравнения (5.74).
Вместо непосредственных вычислений по формуле (5.26) методом Рунге-Кутта определяют четыре числа:
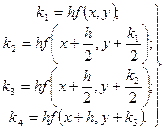 (5.78)
(5.78)
Можно доказать, что если числам 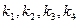 придать соответственно веса 1/6; 1/3; 1/3; 1/6, то средневзвешенное этих чисел, т.е.
придать соответственно веса 1/6; 1/3; 1/3; 1/6, то средневзвешенное этих чисел, т.е.
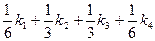 (5.79)
(5.79)
с точностью до четвертых степеней равно значению  , вычисленному по формуле (5.77):
, вычисленному по формуле (5.77):
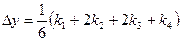 . (5.80)
. (5.80)
Таким образом, для каждой пары текущих значений 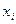 и
и 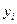 по формулам (5.27) определяют значения
по формулам (5.27) определяют значения
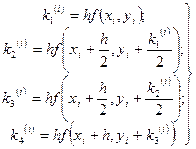 (5.81)
(5.81)
Метод Рунге-Кутта имеет порядок точности 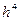 на всем отрезке [а,b]. Оценка точности этого метода очень затруднительна. Грубую оценку погрешности можно получить с помощью "двойного просчета" по формуле
на всем отрезке [а,b]. Оценка точности этого метода очень затруднительна. Грубую оценку погрешности можно получить с помощью "двойного просчета" по формуле
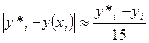 , (5.82)
, (5.82)
где 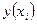 - значение точного решения уравнения (5.74) в точке
- значение точного решения уравнения (5.74) в точке 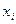 а
а  и
и 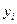 - приближенные значения, полученные с шагом h/2 и h.
- приближенные значения, полученные с шагом h/2 и h.
Если 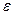 - заданная точность решения, то число n (число делений) для определения шага интегрирования
- заданная точность решения, то число n (число делений) для определения шага интегрирования 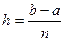 выбирается таким образом, чтобы
выбирается таким образом, чтобы
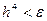 . (5.83)
. (5.83)
Однако шаг расчета можно менять при переходе от одной точки к другой.
Для оценки правильности выбора шага h используют равенство
 , (5.84)
, (5.84)
где q должно быть равно нескольким сотым, в противном случае шаг h уменьшают.
Метод Рунге-Кутта может быть применен и к решению систем дифференциальных уравнений.
Пусть задана система дифференциальных уравнений первого порядка
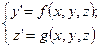 (5.85)
(5.85)
с начальными условиями
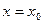 ,
,  ,
,  . (5.86)
. (5.86)
В этом случае параллельно определяются числа 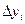 и
и 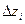 :
:
 (5.87)
(5.87)
где 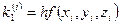 ;
;
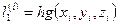 ;
;
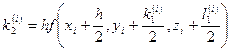 ;
;
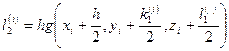 ;
;
 ;
;
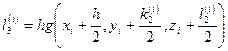 ;
;
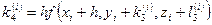 ;
;
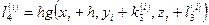 .
.
Тогда получим решение системы
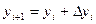 ,
, 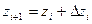 . (5.88)
. (5.88)
Дата добавления: 2015-11-06; просмотров: 11683;
