Глава 8. Численное интегрирование

Если функция 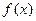непрерывна на отрезке 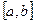и известна ее первообразная 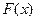, то определенный интеграл от этой функции в пределах от a до b может быть вычислен по формуле Ньютона-Лейбница:

,

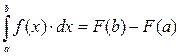где 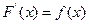. Однако, во многих случаях первообразная функция не может быть найдена с помощью элементарных средств.

Данную функцию 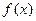на рассмотренном отрезке 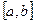заменяют интерполирующей или аппроксимирующей функцией 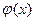простого вида (например, полином), а затем приближенно полагают

.

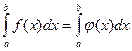Функция 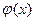должна быть такова, чтобы 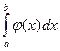вычислялся непосредственно. Если функция 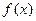задана аналитически, то ставится вопрос об оценке погрешности этой формулы.