Метод наименьших квадратов для полиномов
Мы рассматривали функции, зависящие от двух параметров. Предположим, что аппроксимирующая функция имеет вид квадратичной зависимости:  .
.
Аналогично линейной зависимости составим функцию
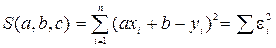 , где
, где 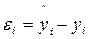 (
( 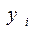 -табличное значение,
-табличное значение, 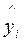 - эмпирическая формула).
- эмпирическая формула).
Возьмем частные производные по a,b и c 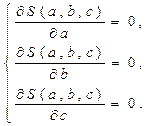
И приравняем их к нулю
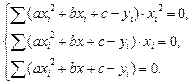
Получим нормальную систему уравнений.
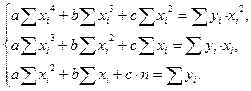 -
-
Решив нормальную систему относительно неизвестных a,b,с, найдём значения параметров приближающей функции.
Если аппроксимирующая функция является многочленом более высокого порядка “n”, то суть подхода к решению задачи не изменится, а увеличится только число уравнений системы.
Пример 7.2.
Данные предыдущего примера 7.1 аппроксимируем квадратичной зависимостью: 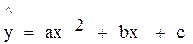 . Напомним условие примера
. Напомним условие примера

|

|
| Задание матрицы коэффициентов нормальной системы и столбца ее свободных членов |

|
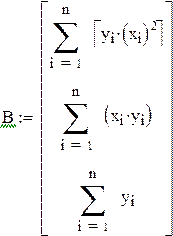
|
| Решение нормальной системы |
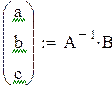
|
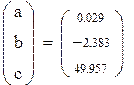
|
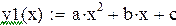
|
|
| сумма квадратов отклонений |

|
| среднеквадратичное отклонение |
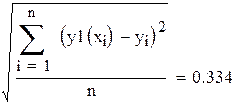
|
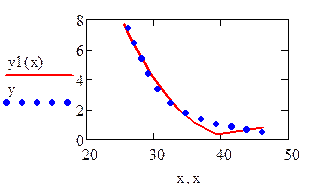
Рис. 7.3. Решение примера 7.2 в Mathcad
Поскольку величина суммы квадратов отклонений для квадратичной зависимости 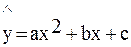 получилась больше, чем у найденной ранее степенной функции, в данном примере предпочтительнее степенная функция.
получилась больше, чем у найденной ранее степенной функции, в данном примере предпочтительнее степенная функция. 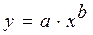
Если аппроксимирующая функция является многочленом более высокого порядка “n”, то суть подхода к решению задачи не изменится, а увеличится только число уравнений системы.
Для построения аппроксимирующей зависимости в виде многочлена в Mathcad можно воспользоваться встроенными функциями regress и interp. Функция regress(x,y,k) возвращает вектор коэффициентов полиномов k-й степени, подобранного методом наименьших квадратов по экспериментальным точкам x и y(x -массив абсцисс, y- массив ординат). Элементы массива x должны быть упорядочены по возрастанию.
Пример 7.3
Продолжим вычисления с данными примера 7.1:

|

|
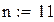
|
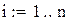
|
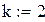
|

|
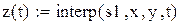
|
| Сумма квадратов отклонений. |
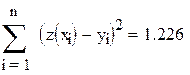
|
| Среднеквадратичное отклонение |
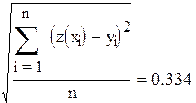
|
Естественно, результаты такие же, как в примере 7.2

|

|

|
| Сумма квадратов отклонений измеренных значений от вычисленных |
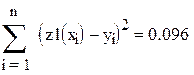
|
| среднеквадратичное отклонение |
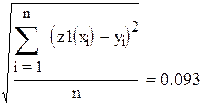
|
Для кубической параболы получился самый хороший результат
Графики практически совпадают, поэтому не имеет смысла брать приближающий многочлен более высокого порядка.
Рис. 7.4. Решение примера 7.2 в Mathcad
Дата добавления: 2015-10-09; просмотров: 673;
