Метод наименьших квадратов. Задача наименьших квадратов возникает в самых различных областях науки и техники, например, при статистической обработке данных.
Задача наименьших квадратов возникает в самых различных областях науки и техники, например, при статистической обработке данных.
Для линейной зависимости y=ax+b составляем функцию, которая представляет собой сумму квадратов отклонений от прямой: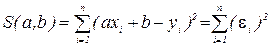 
, где 
( 
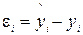-табличное значение,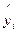 
- эмпирическая формула). Надо определить такие значения параметров a и b , при которых функция двух переменных достигает минимума. Необходимым условием для этого является равенство нулю частных производных по a и b.
Возьмем частные производные по переменным a и b, приравняем их к нулю:
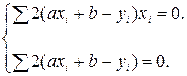
Получим систему линейных уравнений относительно неизвестных
a и b. Система называется нормальной для метода наименьших квадратов. Решаем систему по правилу Крамера:
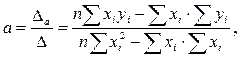
Если обозначить: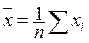 
, 
,
, 
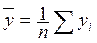, то тогда можно записать
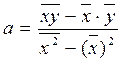и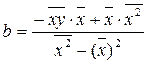 
.
Дата добавления: 2015-10-09; просмотров: 618;