Построение эмпирической формулы.

Пусть в результате измерений в процессе опыта получена таблица некоторой зависимости y(x).

Требуется подобрать формулу, которая выражает данную зависимость аналитически. Такая формула называется эмпирической.

Мы уже рассматривали один из подходов к решению данной задачи, он состоит в построении интерполяционного многочлена, значения которого будут совпадать в точках x_i с соответствующими табличными значениями f(x_i), где i=1,2..n. Но совпадения значений в узлах может вовсе не означать совпадение характеров исходной и интерполирующей функции. Требование совпадения значений тем более не оправдано, если значение функции f(x) известны с некоторой погрешностью. Поставим задачу так, чтобы с самого начала находить функцию заданного вида 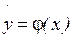, которая в точках x_1, x_2… x_n принимает значения как можно более близкие к табличным значениям y_1, y_2… y_n . Так как точную функциональную зависимость подобрать достаточно сложно, выбирают простые по виду аналитические функции, а затем устанавливают параметры этой функции. Самая простая линейная зависимость 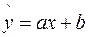, у неё два параметра а и b . Подберем их различными методами.