Кубические сплайны
При рассмотрении изгиба изогнутость приходится представлять кривой более высоких порядков. В этом случае часто применяют кубические сплайн функции, когда функция 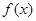 интерполируется на каждом элементарном отрезке кубическим многочленом. На отрезке
интерполируется на каждом элементарном отрезке кубическим многочленом. На отрезке 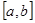 оси Ox зададим равномерную сетку с шагом
оси Ox зададим равномерную сетку с шагом 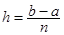 , в узлах
, в узлах 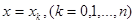 зададим значения
зададим значения 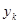 функции
функции 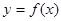 , определенной на отрезке
, определенной на отрезке 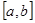 .
.
Внутри каждого элементарного отрезка 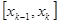 заменим функцию
заменим функцию 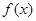 функцией
функцией 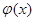 , удовлетворяющей следующим условиям:
, удовлетворяющей следующим условиям:
1. 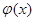 непрерывна на
непрерывна на 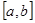 вместе со своими производными первого и второго порядка;
вместе со своими производными первого и второго порядка;
2. 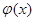 на каждом отрезке
на каждом отрезке 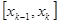 является кубическим многочленом:
является кубическим многочленом:
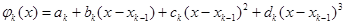 (6.1) ;.
(6.1) ;.
3. в узлах сетки 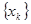 выполняется равенство
выполняется равенство 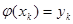 ;
;
4. 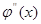 удовлетворяет граничным условиям
удовлетворяет граничным условиям 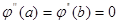 .
.
Требуется найти четверку неизвестных коэффициентов 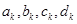 для всех
для всех 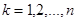 Можно доказать, что задача нахождения кубического сплайна имеет единственное решение.
Можно доказать, что задача нахождения кубического сплайна имеет единственное решение.
Потребуем выполнения третьего условия, совпадения значений функции 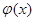 в узлах с табличными значениями;
в узлах с табличными значениями;
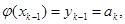 (6.2)
(6.2)
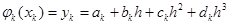 (6.3)
(6.3)
Число полученных уравнений 2n в два раза меньше числа неизвестных коэффициентов. Для составления оставшихся уравнений воспользуемся первым условием о непрерывности производных сплайна во всех точках. Приравняем левые и правые производные во внутреннем узле xk 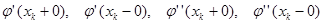 , вычислив предварительно выражение для производных
, вычислив предварительно выражение для производных 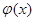 последовательным дифференцированием (6.1)
последовательным дифференцированием (6.1)
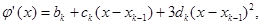 (6.4)
(6.4)
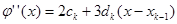 (6.5)
(6.5)
Найдем правые и левые производные в узле:
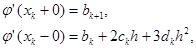
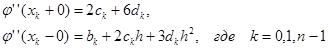
Приравняв левые и правые производные, получим для:
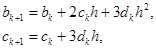
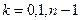 (6.6)
(6.6)
Уравнения (6.6) дают еще 2(n-1) условий. Для получения недостающих уравнений накладывают требования к поведению сплайна на концах отрезка 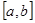 . При нулевой кривизне, когда вторая производная равна нулю, например, получим:
. При нулевой кривизне, когда вторая производная равна нулю, например, получим:
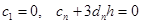 (6.7)
(6.7)
Исключив из уравнений (6.2)- (6.6) неизвестные ak, получим систему из 3n уравнений:
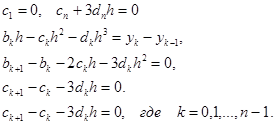 (6.8)
(6.8)
Решив эту систему, мы найдем значения неизвестных ak,bk,ck определяющих совокупность формул для искомого интерполяционного сплайна
Для вычисления коэффициентов сплайнов в Mathcad предназначены функции, возвращающие массив коэффициентов:
cspline(x,y)-кубического сплайна;
pspline(x,y)-квадратичного сплайна;
lcspline(x,y)-линейного сплайна;
Во всех этих функциях х-массив абсцисс , а y- массив ординат экспериментальных точек. После вычисления коэффициентов сплайнов можно вычислить значение интерполяционного полинома в конкретной точке t, обратившись к функции interp(x,U,P,t), где х- массив коэффициентов сплайнов
Пример 6.1 В результате опыта холостого хода определена таблица зависимости потребляемой из сети мощности P от выходного напряжения U для асинхронного двигателя. Построить график интерполяционной зависимости. При решении воспользуемся встроенными функциями сплайновой аппроксимации в Mathcad
Экспериментальные точки



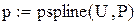






Построим графики этих функций.

Рис 6.1. Решение примера 6.1 в Mathcad
Дата добавления: 2015-10-09; просмотров: 1211;
