Дифференцирование неявной функции
Если независимая переменная  и функция
и функция 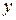 связаны уравнением вида
связаны уравнением вида 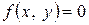 , которое не разрешено относительно
, которое не разрешено относительно 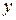 , то
, то 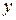 называется неявной функцией
называется неявной функцией  . Нахождение производной функции, заданной неявно, заключается в том, что обе части уравнения
. Нахождение производной функции, заданной неявно, заключается в том, что обе части уравнения 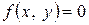 дифференцируются по
дифференцируются по  . С учетом того, что
. С учетом того, что 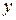 есть функция
есть функция  , и из полученного уравнения определяется
, и из полученного уравнения определяется 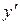 .
.
Пример. Найти производную 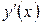 от функции, заданной неявно
от функции, заданной неявно 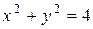 .
.
Решение. Так как 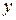 является функцией от
является функцией от  , то будем рассматривать
, то будем рассматривать 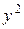 как сложную функцию от
как сложную функцию от  . Следовательно
. Следовательно 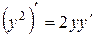 . Продифференцировав по
. Продифференцировав по  обе части данного уравнения, получим:
обе части данного уравнения, получим:
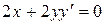 ,
, 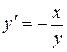 .
.
Пример. Найти 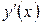 , если
, если 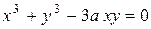 .
.
Решение. При дифференцировании последнего слагаемого надо применить формулу для дифференцирования произведения и тогда
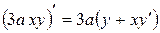 .
.
Поэтому получаем
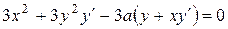 .
.
Сокращаем на 3, раскрываем скобки, переносим члены, не содержащие 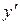 , в правую часть равенства и получаем
, в правую часть равенства и получаем
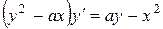 ,
,
отсюда
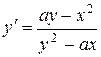 .
.
| 3. Применение производной к исследованию функции |
Понятие производной удобно применять для аналитического исследования свойств функции и построения ее графика.
Областью определения функции 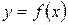 называют множество значений аргумента
называют множество значений аргумента  , при которых функция определена.
, при которых функция определена.
Функция 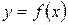 называется четной, если выполняется условие
называется четной, если выполняется условие 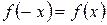 . При этом график функции симметричен относительно оси
. При этом график функции симметричен относительно оси 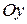 . Функция
. Функция 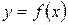 называется нечетной, если выполняется условие
называется нечетной, если выполняется условие 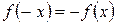 . При этом график функции симметричен относительно начала координат точки
. При этом график функции симметричен относительно начала координат точки 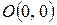 . Если функция
. Если функция 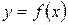 не является ни четной, ни нечетной, то эта функция общего вида. Функция
не является ни четной, ни нечетной, то эта функция общего вида. Функция 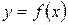 называется периодической с периодом
называется периодической с периодом 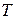 , если выполняется условие
, если выполняется условие 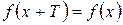 .
.
Функция 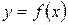 называется возрастающей на некотором интервале, если для любых двух чисел
называется возрастающей на некотором интервале, если для любых двух чисел  и
и 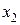 из этого интервала из неравенства
из этого интервала из неравенства 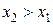 следует неравенство
следует неравенство 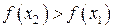 .
.
Функция 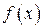 называется убывающей на некотором интервале, если для любых двух чисел
называется убывающей на некотором интервале, если для любых двух чисел  и
и 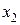 из этого интервала из неравенства
из этого интервала из неравенства 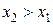 следует неравенство
следует неравенство 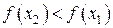 .
.
Возрастающие или убывающие функции называются монотонными.
Дата добавления: 2015-09-28; просмотров: 2167;
