Производная сложной функции. Если , а является функцией независимой переменной : , то называется сложной функцией переменной
Если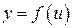 
, а 
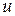является функцией независимой переменной 
: 
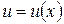, то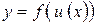 
называется сложной функцией переменной 
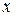. Переменная 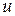при этом называется промежуточной. Производная по функции 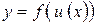имеет вид 
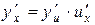. Аналогичное правило имеет место и в случае, когда сложная функция задается цепочкой, содержащей три и более звена. Например, если 
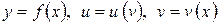, то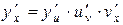 
. Практическую реализацию этого правила покажем на примерах.
Пример. Найти производную функции 
.
Решение. Дифференцируем сначала тангенс, учитывая, что роль промежуточного аргумента выполняет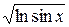 
. Получим 
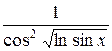. Теперь мысленно зачеркнем значок “ 
” и видим перед собой выражение 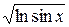. Дифференцируем корень: 
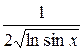и мысленно закрываем значок корня. Остается 
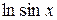. Дифференцируем логарифм (промежуточным аргументом является 
): 
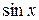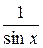. После вычеркивания значка “ 
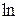” появляется 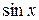, что при дифференцировании даст 
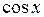. Теперь 
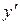запишется в виде произведения всех промежуточных результатов дифференцирования:
.
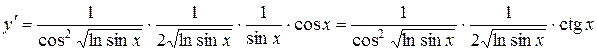Пример.Найти производную функции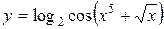 
.
Решение.
=
.
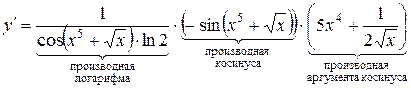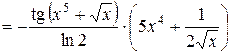Пример. Найти производную функции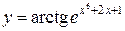 
.
Решение. Применяя правило дифференцирования сложной функции и суммы, получим
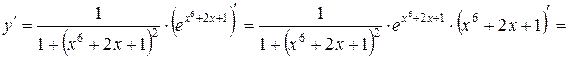
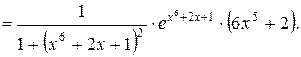
Дата добавления: 2015-09-28; просмотров: 607;