Признаки возрастания и убывания функции
Следующая теорема выражает важный для практических целей признак строгого возрастания и строгого убывания функции и указывает правило для определения интервалов, на которых функция возрастает и убывает (интервалов монотонности функции).
| Теорема. | (достаточный признак возрастания и убывания функции на интервале)
Если во всех точках некоторого интервала первая производная 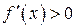 , то функция , то функция 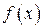 на этом интервале возрастает.
Если же во всех точках некоторого интервала первая производная на этом интервале возрастает.
Если же во всех точках некоторого интервала первая производная 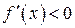 , то функция на этом интервале убывает. , то функция на этом интервале убывает.
|
Правило. Для определения интервалов строгого возрастания и строгого убывания функции следует решить неравенства:
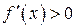 и
и 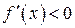 .
.
Пример. Найти интервалы монотонности функции
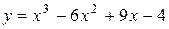 .
.
Решение. Областью определения данной функции является вся ось 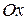 . Находим производную
. Находим производную 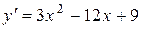 . Чтобы найти интервалы возрастания функции, решим неравенство
. Чтобы найти интервалы возрастания функции, решим неравенство 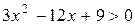 или
или 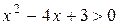 ; чтобы найти интервалы убывания функции, решим неравенство
; чтобы найти интервалы убывания функции, решим неравенство 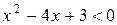 . Корни квадратного трёхчлена
. Корни квадратного трёхчлена 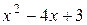 равны 1 и 3, поэтому распределение знаков квадратного трехчлена имеет вид
равны 1 и 3, поэтому распределение знаков квадратного трехчлена имеет вид
+ – +
 |
1 3 
Следовательно, на интервалах 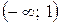 и
и 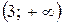 функция возрастает, а на интервале
функция возрастает, а на интервале 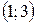 функция убывает.
функция убывает.
Дата добавления: 2015-09-28; просмотров: 837;
