Асимптоты
| Определение. | Если расстояние от кривой 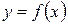 , имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой от начала координат в бесконечность, стремится к нулю, то прямая называется асимптотой данной кривой. , имеющей бесконечную ветвь, до некоторой определенной прямой по мере удаления точки по этой кривой от начала координат в бесконечность, стремится к нулю, то прямая называется асимптотой данной кривой.
|
Различают асимптоты: вертикальные и наклонные.
1. Кривая 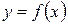 имеет вертикальную асимптоту
имеет вертикальную асимптоту 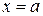 , если при
, если при 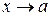 ,
, 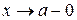 или при
или при 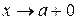
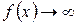 . Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых
. Для определения вертикальных асимптот надо отыскать те значения аргумента, вблизи которых 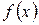 неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются
неограниченно возрастает по абсолютной величине. Если такими значениями аргумента являются 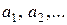 , то уравнения вертикальных асимптот будут
, то уравнения вертикальных асимптот будут
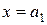 ;
; 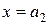 ; …
; …
Вертикальные асимптоты – это нули знаменателя функции. Например, 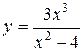 . Здесь две вертикальные асимптоты:
. Здесь две вертикальные асимптоты: 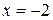 ,
, 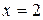
2. Для определения наклонной асимптоты 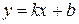 кривой
кривой 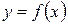 надо найти числа
надо найти числа 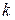 и
и 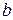 по формулам
по формулам
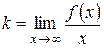 ,
, 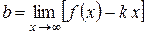
(иногда следует отдельно рассматривать случаи 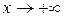 и
и 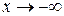 ).
).
Дата добавления: 2015-09-28; просмотров: 643;
