Асимптоты графика функции. Построение графика функции значительно облегчается, если знать его асимптоты.

Построение графика функции значительно облегчается, если знать его асимптоты.

Определение.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).

Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.

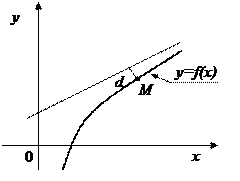Рис. 5.10

Вертикальные асимптоты

Определение.

Прямая 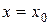называется вертикальной асимптотой графика функции 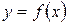, если выполнено одно из условий:

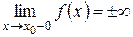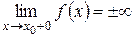или (рис.5.11)

Рис. 5.11

Вертикальные асимптоты, уравнение которых х=x₀ , следует искать в точках, где функция терпит разрыв второго рода, или на концах ее области определения, если концы не равны 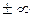. Если таких точек нет, то нет и вертикальных асимптот.

Например, для кривой 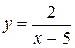, вертикальной асимптотой будет прямая 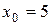, так как 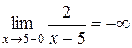, 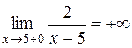. Вертикальной асимптотой графика функции 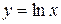является прямая 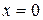(ось Оу), поскольку

.

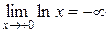Горизонтальные асимптоты

Определение.

Если при 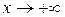( ) функция имеет конечный предел, равный числу b:

,

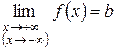то прямая 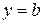есть горизонтальная асимптота графика функции .

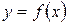Например, для функции имеем

, .

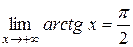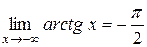Соответственно, прямая 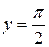− горизонтальная асимптота для правой ветви графика функции , а прямая 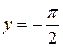− для левой ветви.

В том случае, если

,

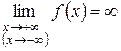график функции не имеет горизонтальных асимптот, но может иметь наклонные.