Горизонтальные асимптоты (перпен оси оу)
Если сущ-ет limх®+¥f(х)=А конечный или limх®-¥f(х)=В- конечный или одновременно, то прямая у=А или у=В или одновременно обе будут горизонтальными асимптотами для кривой у= f(х), т.к. limх®+¥d= limх®+¥ (f(х)-А)=А-А=0. Аналогично для другой
Пример.
У=(1,2)х. limх®-¥ (1,2)х =0. у=0, те ось ох есть горизонтальная асимптота.
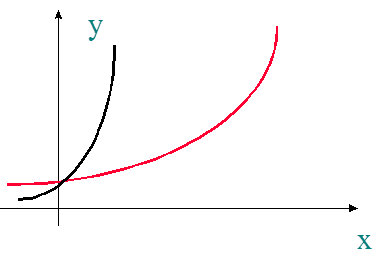
Нужно проверять и при х®¥ и при х®-¥, тк могут быть две горизонтальные и разные.
Как для у=arctg x, у=П/2, у=-П/2.
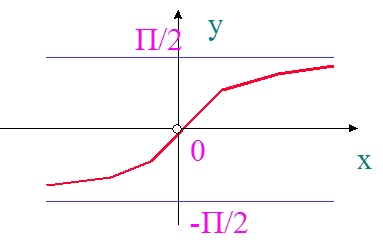
3.Наклонные асимптоты ( не параллельные оси оу).
Пусть кривая у= f(х) им. наклонную асимптоту У=кх+в. Возьмем на кривой произвольную точку М(х,у).
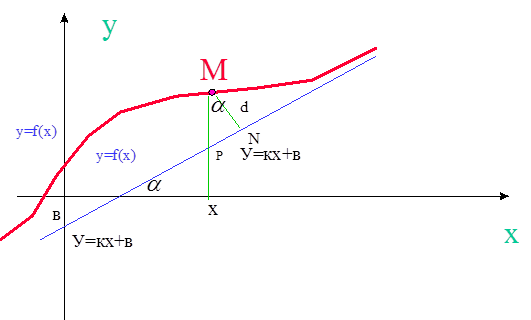
Из треугольника MNP видно, что d=МР*cosa=(у-У)* cosa.
a=const, поэтому условие d®0 равносильно условию у-У®0,те limх®¥(у-У) или limх®¥(f(х)-кх-в)=0, (1).
Условие (1) явл. необходимым и достаточным для того, чтобы прямая у=кх+в была наклонной асимптотой для кривой у= f(х). Как найти к и в по функции у= f(х)?
Из (1) следует limх®¥((f(х)-кх-в))/х=0 или limх®¥(f(х)/х-к)=0, тк в/х®0 при х стрем. к бесконечности.
Но тогда к= limх®¥f(х)/х, (2). Из (1) следует, что в= limх®¥(f(х)-кх), (3).
Зная к и в находим уравнение наклонной асимптоты у=кх+в.
Совершенно аналогично находится наклонная асимптота при х стрем к минус бесконечности, справедливы те же ф-лы (1)-(3) с заменой х®¥ на х®-¥. Проверять нужно оба случая, т.к. возможны две разные асимптоты для двух бесконечных ветвей функции.
Замечание:
1)при к=0 , limх®±¥f(х)=в, те получаются горизонтальные асимптоты. Поэтому можно искать сразу наклонные асимптоты. Горизонтальные получаются при этом автоматически (если они есть), 2)при к=¥ или в=¥ наклонных асимптот нет.
Пример. f(х)=1/х+х. Найти асимптоты. Х=(-¥,0)+(0, ¥).
1)Вертикальные асимптоты могут быть лишь в т.х=0- она граничная и явл точкой разрыва limх®0-0(1/х+х)= -¥, limх®0+0(1/х+х)= ¥. Значит х=0- вертикальная асимптота.
2)Наклонные асимптоты У=кх+в.
к= limх®¥f(х)/х= limх®¥(1/х2+1)=1, к=1,
в= limх®¥(1/х+х-1х)=0, в=0,
у=х- наклонная асимптота.
При х®-¥ получим тоже к=1, в=0, т.е. ту же асимптоту у=х.
§6.Полное исследование функции и построение ее графика
Обычно при построении графика функции у=f(х) используют метод построения по точкам, когда из области определения берут несколько значений аргумента х1,х2...хn, вычисляют соответствующие значения функции у1,у2...уn, строят точки (х1,у1), (х2,у2), …,( хn, уn) и соединяют их плавной кривой. В простых случаях полученная линия достаточно точно изображает настоящий график функции у=f(х). Но если функция f(х) им. особенности, разные возрастания и убывания, разрывы и т.п., то полученный чертеж может быть далек от истины.
Для построения точного графика нужно знать его особенности. Это позволяет сделать дифференциальное исчисление. Суть метода в том, что находят характерные опорные точки графика (а не случайные) и соединяют их с учетом особенностей его, а не просто плавной кривой линией.
Для исследования функции и построения графика нужно проделать следующую работу:
-определить область существования функции. Это сразу выявит т.е. значения аргумента, над которыми кривая графика проходит и над какими нет,
-исследовать ф-ию на периодичность, четность, нечетность Это позволит (если функция обладает этими св-ми) строить график лишь в части обл. сущ-ия, а в другой достроить его автоматически,
-исследовать ф-ию на непрерывность, определить ее точки разрыва,
-найти экстремумы функции и участки ее возрастания и убывания,
-определить точки перегиба функции, участки выпуклости и вогнутости графика,
-найти асимптоты графика,
-определить точки пересечения графика с осями координат,
-исследовать ф-ию около точек границы ее области сущ-ия,
-если ход графика в отдельных местах недостаточно ясен, взять несколько дополнительных точек.
Для удобства результаты заносят в таблицу вида
| х | ||||
| у | ||||
| особенности |
Полученные опорные точки из таблицы переносят на плоскость и соединяют с учетом всех особенностей функции. В некоторых случаях для удобства по осям берут разные масштабы.
Пример полного исследования функции и построение графика.
Построить график функции у=f(х)= 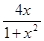 .
.
1.обл определения функции (-¥,¥),
2.функция нечетная f(-х)=-f(х), (достаточно построить график для х³0), не явл периодической,
3.функция непрерывна в (-¥,¥) как частное двух непрерывных, знам не равен 0, график есть сплошная линия,
4.исследуем на экстремум, у'=4 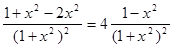 ,
,
у''=4 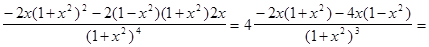
=4 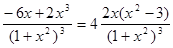 ,
,
у''= 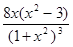 .
.
Критические точки у'=0, 1-х2=0, х1=-1, х2=1, других нет.
у"(-1)>0, min,
у"(1) <0,max,
уmin=-2 при х=-1, уmax=2 при х=1,
(-¥,-1), у'<0- кривая убывает
(-1,1), у'>0- кривая возрастает,
(1, ¥), у'<0- кривая убывает.
5.точки подозрительные на перегиб. у"=0.
х1=0, х2=- 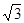 , х3=+
, х3=+ 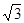 - других нет.
- других нет.
(-¥,- 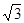 ), у"<0-кривая выпуклая,
), у"<0-кривая выпуклая,
(- 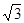 ,0), у">0 -кривая выгнутая.
,0), у">0 -кривая выгнутая.
Отсюда х2=- 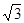 =-1,73- точка перегиба
=-1,73- точка перегиба 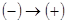
х3= 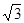 - точка перегиба
- точка перегиба 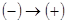
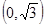
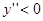 кривая выпуклая
кривая выпуклая
x1=0-точка перегиба 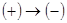
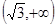
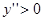 кривая вогнутая
кривая вогнутая
6.находим асимптоты, вертикальных нет. Находим наклонные.
у=кх+в, к= limх®±¥f(х)/х= limх®±¥ 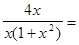 0, к=0,
0, к=0,
в= limх®±¥(f(х)-кх)= limх®±¥( 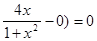 , в=0. Асимптота у=0- горизонтальная, ось ох (и при
, в=0. Асимптота у=0- горизонтальная, ось ох (и при 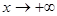 и при
и при 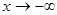 ).
).
7.точки пересечения с осями: х=0, у=0- кривая проходит через начало координат,
8.на границе обл. сущ-ия, те при х®-¥, х®¥, у=f(х) ®0, кривая приближается к оси ох. Составим таблицу:
| х | ®-¥ | -1,73 | -1 | 1,73 | ®¥ | |||
| у | ®0 | -1,73 | -2 | 1,73 | ®0 | 6/5 | ||
| особен | у=0, асимп | перегиб | min | перегиб | max | перегиб | у=0, асимп |
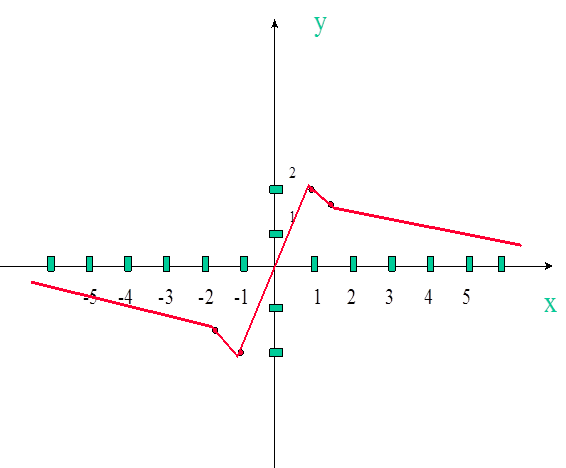
Чертим график.
Дата добавления: 2015-10-05; просмотров: 1134;
