Исследование функций с помощью производных. Простроение графиков функций.

§1.Условия постоянства, возрастания и убывания функций

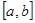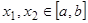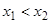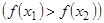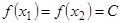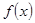При изучении характера изменения функции и ее графика на первом месте стоит вопрос, при каких условиях функция сохраняет в данном промежутке постоянное значение или меняется монотонно? Для простоты промежуток будем считать сегментом. Напомним, что на функцию называют возрастающей (убывающей), если для любых из условия следует . Если всегда , то называется постоянной на 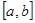. 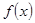называют неубывающей (невозрастающей) на 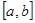,если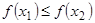

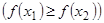
Ответ на вопрос дают следующие теоремы.

Теорема 1.

Пусть функция у=f(x) определена и непрерывна на [а,в], и на (а,в) имеет конечную производную f '(x).

Для того чтобы f(x) была постоянной на [а,в], Н. и Д., чтобы f '(x)=0 на [а,в].

Доказательство.

1. Достаточность

Пусть f '(x)=0 при xÎ(а,в). Возьмем произв. [а,х] где а<х£в. На [а,х] функция f(x) удовлетворяет всем условиям т-мы Лагранжа. Тогда сущ. т.c а<c<х, что f(x)-f(а)=(х-а)*f '(с). Но f '(с)=0 отсюда f(x)=f(а)= const для любого х Î(а,в).

2.Необходимость

Пусть f(x)= С=const для любого х Î(а,в). Но тогда f '(x)=C '=0 на (а,в).

Теорема 2.

Пусть функция у=f(x) определена и непрерывна на [а,в], и в (а,в) им. конечную произв f '(x). Для того чтобы функция f(x) была неубывающей (невозрастающей) на [а,в], Н. и Д., чтобы для всех xÎ(а,в) было f '(x)³0 ( f '(x)£0).

Д-во проведем для случая неубывающей функции (для невозрастающей сам-но).

1. Достаточность

Пусть f '(x)³0 на [а,в],те для люб. хÎ(а,в).

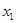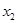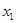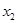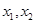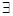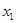Возьмем две произвольные точки и Î[а,в] при чем а£ < £в. На [ ] функция удовл. всем условиям т-мы Лагранжа, поэтому С <С< 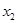, что 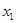f( )-f( 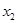)= f '( c )( 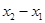)³0 отсюда 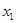f( )³f( 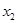), что и показывает неубывание f(х) на [а,в].

2.Необходимость.

Пусть f(x) неубывает на [а,в]. Это значит , что для любых точек и +Dх (считаем Dх>0), принадлежащих [а,в] им место f( +Dх)-f( )³0Þ f( +Dх)-f( ))/ Dх³0. Но тогда и lim_C®C0 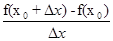³0, те f '( )³0, т.к. т. - любая из (а,в), то необходимость тоже доказана.

Теорема 3.

Пусть функция у=f(x) определена и непрерывна на [а,в] и им конечную производную f '(x) на (а,в).

Для того, чтобы функция у=f(x) была возрастающей (убывающей), достаточно выпол. условия f'(x)>0 (f'(x)<0) для люб. х принад. (а,в).

Доказательство для возрастания аналогичное док-ву достаточности в Т-ме 2, только нестрогое неравенство везде следует заменить на строгое >. (Для убывания аналогично).

Замечание. Из т-мы 3 следует, что строгое возрастание функции вытекает из f'(x)>0.

Наоборот не всегда верно: даже для строго возрастающей функции производная может обращаться в ноль. Те f'(x)³0 только.

Пример: у=х³ возрастает на [-1,1], но в т. х=0 у'(0)=3х² 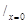=0. Касательная параллельна оси ох.

Вывод: касательная и к графику возрастающей функции может быть парал. оси ох.

Доказанные теоремы имеют простой геометрический смысл.

Т.к. f'(x) означает угловой коэффициент касательной к графику функции у=f(x) в точке с абсциссой х то в случае f'(x)>0 касат. к графику наклонена под острым углом к оси ох- кривая возрастает, в случае f'(x)<0 касат. наклонена под тупым углом к ох- кривая убывает. Если f'(x)=0 , то в точке касат. параллельна оси ох.

Пример: Исследовать на монотонность ф-ю : 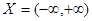- область определения. . Для x<0 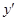<0 – ф-я убывает, для x>0 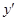>0 – ф-я возрастает.

§2.Экстремумы функций

В первом пункте мы рассмотрели непрерывную на [а,в] ф-ию, явл. монотонной. Пусть теперь на [а,в] определена и непрерывна функция , которая монотонной не является. Тогда обязательно внутри [а,в] найдется точка ( возможно и несколько) , такая ,что в ней значение f( ) явл. наибольшим или наименьшим по отношению к значениям ее в достаточно малой окрестности этой точки ( -d, +d).

Как видим, такие точки графика явл. вершинами горбов или впадин. Характерно, что с одной стороны т. в пределах d-окрестности функция возрастает, а с другой убывает (для 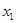- наоборот). Для таких точек вводятся специальные опред.

Определение 1. Говорят что функция у=f(x) им. в точке максимум (минимум), если эту точку можно окружить такой окрестностью ( -d, +d)Î[а,в] , что для всех х из нее выполняется неравенство f(x)£f( ) , (f(x)³f( )).

Обозначают минимум -min, максимум- max. Саму т назыв. точкой максимума или точкой минимума.

Если сущ. такая окрестность точки, что для х¹ в ней выполняется строгое неравенство f(x)<f( ), (f(x)>f( )), то говорят,что функция им. в т. собственный max (min), в противном случае - несобственный.

Min и max объединяют одним понятием- экстремум. Само определение экстремума показывает их возможное существование лишь во внутренних точках обл. определения функции и не может сущ. экстремум в граничных точках.

Точки экстремума нельзя смешивать с точками, где функция принимает свое наибольшее или наименьшее значение для всей области определения функции. Min и max явл. наиб. и наим. значениями функции лишь в достаточно малых окрестностях.

Вполне возможно, что min в одной точке больше max в другой. Так 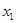f( )>f( 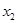), хотя в т 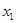- Min , а в 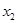- max функции у=f(x).

Однако ,если непрерывная функция им несколько минимумов и максимумов на [а,в], то наибольшее и наименьшее значение функции на [а,в] находится среди них или на концах сегмента. Поэтому нужно уметь находить точки экстремумов.

Делают это спомощью производных.

y

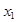
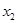
x

Теорема (неоходимое условие экстремума).

Если дифференцируемая (им. конечную производную) функция у=f(x) имеет экстремум в т. ,то ее производная в этой точке равна 0: f'(x)=0

Доказательство.

Т.к. в т. функция им. экстремум, то найдется окрестность ( -d, +d), в которой f( ) явл. наибольшим или наименьшим значением функции f(х). Но тогда по т-ме Ферма f'( )=0.

Условие т-мы , действительно, лишь необходимое, оно не явл достаточным. Так для функции у=х³ в т.х0=0 , у'(0)=0, однако экстремума нет, функция монотонно возрастает.

Итак, теорема утверждает, что экстремум может быть у дифференцируемой функции лишь в тех точках, где производная обращается в ноль, но не обязательно в каждой.

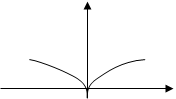
Но экстремумы функция может иметь и в точках, где производная не существует вовсе или равна бесконечности.

Пример.

1) f(x)=|x|. Не имеет производной в т. =0 (касательная не сущ-ет вовсе. Однако в т.х0=0 функция имеет min.

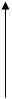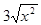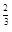2)у=f(x)= =х , у'= 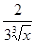, f '(0)=¥. Касательная к графику параллельна оси оу (сама ось oy).

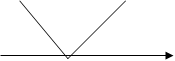Точки ,где касательная вообще не сущ. , назыв. угловыми точками кривой, где касательная параллельна оси оу и кривая заостряется- точками возврата кривой в отличие от случая, где экстремума нет.

Определение 2.

Внутренние точки области определения функции у=f(x), где производная f'(x) обращается в ноль, бесконечность или не существует, называются критическими. Критические точки явл. подозрительными на экстремум, лишь в них возможен экстремум.. Для проверки и отбора точек, где действительно достигается экстремум установим достаточные условия.

Теорема (1-ое достаточное условие экстремума)

Если при переходе через критическую точку производная функции f'(x) меняет знак, то в критической точке функция им. экстремум, а именно max, если производная меняет знак с + на -, min, если с - на +.

Если же производная при переходе через т. знака не изменяет , то в экстремума нет.

Доказательство.

Условие т-мы предполагает существование конечной производной в некоторой окрестности критической точки ( -d, +d), за исключением , быть может самой т. .

При этом в пределах этой окрестности слева от и справа производная сохраняет постоянный знак.

Возможны три случая.

1)Для х< , f'(x)>0, в[ -d, ]-функция возрастает, для х> , f'(x) <0, (с + на -)в [ , +d]- функция убывает, и потому для любого хÎ( -d, +d), f( )³f(x),те в т. max.

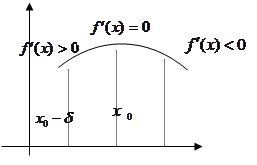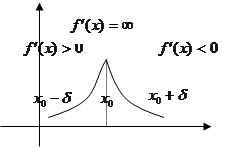x₀₊d

2)Для х< , f'(x) <0, в[ -d, ]-функция убывает, (с - на +)

для х> , f'(x)>0, в [ , +d]- функция возрастает и потому для любого хÎ( -d, +d), f( )£f(x), в т. min

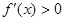
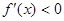
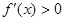
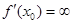
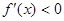
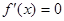
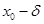
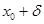
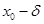
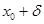
3) f'(x)>0 и для х<х0 и для х>х0, функция возрастает во всей окрестности (х0-d,х0+d), ( 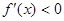аналогично, самостоятельно)

Для х< , f(x) <f( ),

для х>, f( ) <f(x)., ни min, ни max.

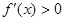
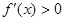
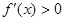
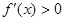
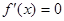
На практике нужно помнить, что знак производной исследуется слева и справа от критической точки в непосредственной близости от нее.

Теорема полностью решает вопрос об экстремумах функции на (а,в), если в нем содержится лишь конечное число критических точек, а между ними производная f '(х) непрерывна. Расположим критические точки в порядке возрастания: а<C₁<C₂<....<C_k-1<Ck<....<C_n<в, (1). В каждом из интервалов (а, 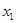), ( , 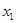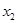),.....,(х_k-1,x_k),....,(x_n,в) производная существует, конечна и не равна нулю, т.к. все иные точки содержаться в (1). На любом интервале (х_k-1,x_k) производная сохраняет знак (это интервал монотонности), т.к. если бы она меняла знак на интервале, то в некоторой точке х_k-1<.С<. x_k. она обращалась бы в 0: f '(С)=0, т.е. нашлась бы новая точка С не учтенная в (1), чего нет.

Значит знак производной в интервале совпадает со знаком производной в некоторой произвольной точке этого интервала. Определив же знаки произ. в интервалах, легко выясним в каких точках есть экстремум и какой именно. Подставляя точки экстремума в значения функции найдем эти экстремумы.

Пример.

Найти экстремумы функции f(х)= 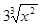-х². Функция определена на (-¥,+¥) и непрерывна.

1) найдем производную: f '(х)=2( -х).

2) определяем критические точки (т.е. где f '(х)=0, ¥, или не сущ-ет).

3) f '(х)= 2( -х).=0, -х=0, 1- =0, =1, х⁴=1. x_1,2=±1.

f '(х)= ¥ в т.х=0. Итак критические точки -1,0,1. В остальных производная непрерывна как разность непрерывных.

4) обл. определения функции разделяем на интервалы (-¥,-1),(-1,0),(0,1),(1,+ ¥) и исследуем знак производной в каждом интервале.

f '(-8)=2(- 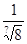+2) >0,+, + +

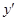– 1 -

f '(-1/8)=2(-2+1/8) <0, -, -1 0 –

f '(1/8)= 2(-2-/8) >0,+,

f(8)=2(1/2-8) <0, -,.

5)Делаем вывод: х=-1, с + на - , max

х=0, с - на +, min,

х=-1, с+ на -, max.

6)Вычисляем экстремальные значения:

f(-1)=3 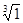-1=2- max,

f(0)=0- min,

f(1)=3 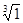-1=2- max,.

Заметим, что одновременно мы нашли промежутки монотонности функции. В (-¥,-1) и (0,1) функция возрастает, в (-1,0) и (1,+ ¥)- убывает.

Замечание. При исследовании критических точек с помощью перемены знака производной нужно помнить, что сама функция в критической точке должна быть определена и непрерывна. Иначе возможна ошибка.

Например, 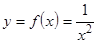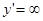в 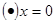меняет знак при переходе через эту точку с 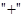на “-“. Должен бы быть 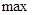! Но функция в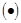 не определена, имеет разрыв.

В некоторых случаях бывает удобнее способ исследования функции на экстремум с помощью следующей теоремы.

Теорема 2.(2-ое достаточное условие экстремума)

Если в критической точке х0 функция у=f(x) дважды дифференцируема и вторая производная в этой точке отличается от нуля , то функция имеет в т.х0 экстремум: max, если f ''(х0) <0 и min, если f ''(х0) >0.

Доказательство.

Т.к. в точке по условию сущ. вторая производная (им. ввиду конечная), то в т. и в некоторой ее окрестности должна тем более существовать производная первого порядка. Т.к. т. - критическая, а f '(х) в ней конечная , то f '( )=0.

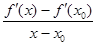По условию в т. сущ. вторая производная функции f (х). По определению второй производной имеем f ''( )=lim_DC®0 , Обозначим +Dх=х, тогда Dх=х- и при Dх®0, x® . Поэтому можем записать f ''( )=lim_C®C0 = lim_C®C0 .

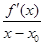Возможны два случая:

1)f ''( ) >0, т.е. lim_C®C0 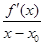>0. Функция 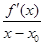явл. непрерывной ф-ией (как частное непрерывных) потому сохраняет знак своего предела для х близких к , т.е. 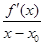>0. Но это возможно если х-х0<0, те х<х0 и f '(х) <0,-,

х-х0>0, те х>х0 и f '(х) >0,+,.

Видим ,что при переходе через т. f '(х) меняет знак с - на +, те в т. - min. Итак: из f ''(х0) >0 следует в т. - min.

2) f ''(х0) <0, т.е. lim_C®C0 <0 след , в некоторой окрестности т.х0 выполняется <0.

3) Но это возможно при х-х0<0, х<х0 и f '(х) >0,+,

прих-х0 >0, х>х0 и f '(х) <0,-,.

Видим ,что при переходе через т.х0 f '(х) меняет знак с + на - след в т.х0-max.

Итак: из f ''(х0) <0, следует, в т.х0- max. ЧТД.

Теорема 2 не дает ответа в случае , когда f ''(х0)=0, экстремум может быть, а может и не быть. Она неприменима и в случае, когда f '(х0) бесконечна или не сущ-ет, т.к. в этом случае о второй производной нет смысла и говорить.

Если f ''(х0)=0, то нужно пользоваться 1-ой теоремой.

Есть еще правило высших производных : если в т.х0 f '(х0)= f ''(х0)=f^(k-1)(х0)=0, а f^(k)(х0) не равно нулю, то если к- нечетное число- экстремума в т.х0 нет, если к- четное, в т.х0 есть экстремум: max, если f^(k)(х0) <0, и min ,если f^(k)(х0) >0,.

Пример.

Найти экстремумы функции у=х³-6х²+9х-4.

Функция определена и непрерывна в (-¥,¥). Находим критические точки.

f '(х)=3х²-12х+9, х²-4х+3=0. 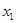=3, 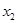=1- других нет.

Находим f ''(х)=6х-12=6(х-2), f ''(3)=18-12=6>0- min в т.х=3,

f ''(1)=6-12=-6<0- max в т.х=1,

f(3)=-4- min значение, f(1)=0- max знач.

Таким образом, видим , что вторая теорема позволяет исследовать знак второй производной в самой т.х0 вместо знака первой производной в окрестности т.х0.

§3.Наибольшее и наименьшее значение функции на отрезке

Значение функции в точке max явл наибольшим лишь в некоторой окрестности этой точки и совсем не обязательно явл. наибольшим значением во всей области определения ф-ии. То же самое можно сказать и о минимуме. В этом случае их назыв часто локальными (местными) max и min в отличии от абсолютных, т.е. - наибольшее и наименьшее знач. во всей обл определения. Если функция f(x) задана на [а,в] и непрерывна на нем, то она достигает на нем в каких либо точках своего наибольшего и наименьшего значений. Как их найти? Если на [а,в] есть несколько max, то наиб. значение внутри (если оно достигается) совпадает с одним из них. В то же время наибольшее значение для всего [а,в] функция может достичь и на одном из концов.

Правило..

Нужно сравнить между собой все min и граничные значения f(а) и f(в). Наименьшее значение и будет наименьшим значением функции на [а,в]. Обычно поступают при нахождении наиб. и наим. значений проще:

1) Находят все критические точки внутри сегмента [а,в], вычисляют значения функции в них ( не определяя есть ли в них экстремум), 2) вычисляют значение функции на концах f(а) и f(в), 3)сравнивают полученные значения между собой: наименьшее значение из этих значений и будет наименьшим значением функции, наибольшее- наибольшим на [а,в].

Пример:

Наити наиб. и наименьшее значение функции у= 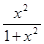на [-1,2],

1.ищем критические точки на (-1,2).

У'= 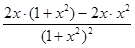=0, 2х+2х³-2х³=0, 2х=0, 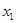=0. Других нет.

f(0)=0,

2. f(-1)=1/2, f(2)=4/5.

3. f(0)=0, наименьшее значение, f(2)=4/5.- наибольшее на

[-1,2].

Нужно заметить следующее. В прикладных задачах наиболее часто встречается случай , когда между а и в функция у=f(x) им. только одну критическую точку. В этом случае без сравнения с граничными значениями ясно, что если в т. max, то это и есть наибольшее значение функции на [а,в], если это min, то это и есть наименьшее значение на [а,в]. Это важно в тех случаях, когда в выражение функции входят буквенные выражения и оказывается более просто исследовать на экстремум, чем сравнивать значения на концах.

Важно отметить, что все сказанное о нахождении наиб и наим значений применимо и к (а,в) и к бесконечному промежутку (-¥,¥), только в этом случае не берут во внимание значения на концах.

§4.Напрвление вогнутости кривой и точки перегиба

Пусть функция у=f(x) им. в т. конечную производную. Тогда она им. в этой точке касательную, уравнение которой есть у- 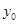= f '( )(х- ) или у=f( )+(х- ) .

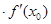В некоторой окрестности ( -d, +d) график функции может располагаться по разному: либо выше касательной, либо ниже , либо с обеих сторон.

Определение.

Говорят, что в т.М( , 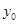) кривая у=f(x) вогнута вниз или просто вогнута (вогнута вверх или выпукла), если для всех х из некоторой окрестности ( -d, +d) точки все точки кривой расположены выше касательной (ниже касательной).

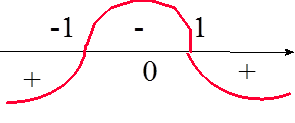
Если в т.М кривая переходит с одной стороны касательной на другую, то т.М назыв. точкой перегиба кривой.

y

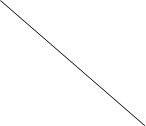
M2

M3

M1

0 x2 x3 x1 x

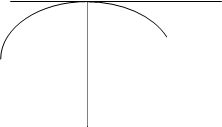
В т.М1- кривая вогнута, М2-выпуклая, М3-перегиб.

В точке перегиба кривая меняет выпуклость на вогнутость или наоборот. Точка перегиба- пограничная между участками выпуклости и вогнутости кривой.

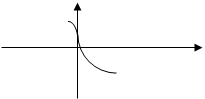
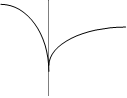
Определение точки перегиба остается в силе и в случае, когда касательная к кривой у=f(x) перпенд. оси ох, те в т. производная f '( )= ¥, и т. не явл. точкой возврата кривой. В отличии от случаев (указанных на чертеже),

y

x x

где т. и х точками перегиба не явл-ся.

Найдем условия, при которых им. место определенное направление вогнутости или перегиб кривой. у=f(x) в произвольной т.х= .

Пусть, например, кривая в т.М( , 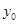) выпуклая. Тогда она располагается в некоторой окрестности ( -d, +d) этой точки ниже касательной у=f( )+f '( )(х- ). Рассмотрим вспомогательную ф-ию j(х)= f(х)-f( )- f '( )(х- ). В т. j( )=0, в d-окрестности т. . Отсюда следует, что в точке функция 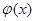имеет max. Значит в точке j''( )£0. Но j''( )= f ''(х) и потому в т. f ''( ) £0.

Таким образом, чтобы в т.х0 кривая у=f(x) была выпуклой необходимо, чтобы f ''( ) £0. Если же в т.х0 f ''( )<0, то в т. - max и кривая, значит, выпуклая. Условие f ''( )<0 достаточное для выпуклости в т. .

Рассуждая совершенно аналогично, получим , что условие f ''( )³0 необходимое для вогнутости в т.х0, а условие f ''( )>0 достаточное для вогнутости.

Вывод:

если в т. вторая производная положительна f ''( )>0, то кривая выгнута в этой точке, если в т. вторая производная отрицательна f ''( )<0, то кривая выпуклая в этой точке.

Удобно правило "чашечки":

В точках перегиба нет определенной вогнутости или выпуклости, а потому они могут быть лишь в точках, где f ''( )=0. Но условие f ''( ) еще не обеспечивает точно, что - точка перегиба. Например, для кривых у=х⁴ и у=-х⁴, в т. f ''( )=0, однако в ней первая кривая вогнута, вторая выпукла.

Вывод: условие f ''( )=0 явл. необходимым условием существования перегиба в т. . Но, как видели, т. перегиба могут быть и там, где вторая производная f''( )=¥ ил не существует вовсе.

Достаточным условием перегиба кривой в т. явл. смена знака второй производной f ''( ) при переходе через т. . При этом , если 2-ая производная меняет при переходе через т. знак с + на - , то в т. перегиб со сменой вогнутости на выпуклость, Если f ''( ) меняет знак с - на + при переходе через т. , то в т. перегиб со сменой выпуклости на вогнутость..

Определение. Если кривая вогнута (выпукла) в каждой точке некоторого промежутка, то она назыв. вогнутой (выпуклой) на этом промежутке.

Исследование функции у=f(x) на выпуклость, вогнутость, точки перегиба проводят по следующему плану:

1.Находят все точки подозрительные на перегиб, для чего:

а) находят второю производную, приравнивают ее к нулю и находят действительные корни полученного уравнения,

б)находят точки, где конечная производная f ''(x) не сущ-ет,

2.Исследуют f ''(х) на изменение знака при переходе через каждую подозрительную на перегиб точку. Если знак меняется- перегиб есть, если нет-то нет.

Для тех точек ,где f ''(х0) >0 кривая вогнута, где наоборот -выпукла. Так же как и в случае экстремумов, если точек подозрительных на перегиб конечное число, пользуются методом интервалов.

Определение.

Если кривая выпукла (вогнута) в каждой точке некоторого промежутка, она назыв. выпуклой (вогнутой) на этом промежутке.

Пример

Исследовать на вып., вогнутость, т. перегиба ф-ию у=х⁴-6х²+5. Обл. опред. Х=(-¥,¥).

1.найдем у'=4х³-12х, у''=12х²-12=12(х²-1), у''=0, х²-1=0, х_1,2=±1-т. подозрительные на перегиб, других нет.

Вся обл. опред. разбивается на интервалы (--¥,-1),(-1,1),(1, ¥), в каждой из них f ''(х) им. постоянный знак, т.к. непрерывна в них. Легко видеть, что в (--¥,-1) +, в (-1,1) -, и в (1, ¥) +. Отсюда ясно, что в т. -1 и 1 перегиб, причем в (-¥,-1) график функции вогнутый, в (-1,1) выпуклый, в (1, ¥) - вогнутый.

§5.Асимптоты кривой (графика функции)

Если функция у=f(x) определена и ограничена на конечном промежутке, то график ее можно построить по нескольким точкам, соединяя их плавной кривой. Но если обл. определения функции бесконечно велика или функция не ограничена, судить о графике по нескольким точкам трудно, т.к. ветви графика уходят в бесконечность. На помощь в этом случае часто приходят асимптоты кривой графика.

Определение.

Прямая линия назыв асимптотой для кривой у=f(x), если расстояния от точки М, лежащей на кривой, до этой прямой стремиться к нулю при движении точки М вдоль какой-нибудь части кривой в бесконечность.

Заметим сразу, что кривая у=f(x) может приближаться к асимптоте как не пересекая ее, так и пересекая.

Различают два вида асимптот: вертикальные, горизонтальные и наклонные.

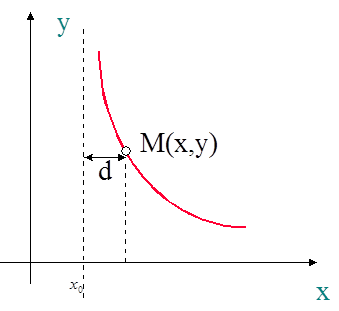
1. вертикальные-(парал оси оу). Из определения ас-от следует, что если lim_х®х0+0f(х)=¥ или lim_х®х0-0f(х)=¥, то прямая х=х0 есть асимптота кривой у=f(x).

Действительно при х® т.М®¥, а расстояние т.М от прямой х=х0, d=|x- |®0.

Верно и обратное, если прямая х=х0 -вертикальная асимптота, то хоть один из односторонних пределов функции в т.х0 равен беск-ти (может и два).

Таким образом , кривая у=f(x) им. вертикальную асимптоту в точках, приближаясь к которым функция стремится к беск-ти. Это либо точки разрыва функции ,либо граничные точки обл. определения.

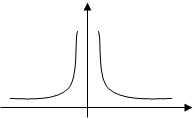
Пример.

У= 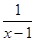, точка разрыва х=1 , lim_х®1-0 =-¥,

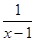lim_х®1+0 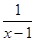=¥, х=1 – вертикальная асимптота.