Наклонные асимптоты графика функции
Теорема 1. Для того чтобы прямая линия 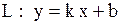 была асимптотой графика функции
была асимптотой графика функции 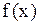 необходимо и достаточно, чтобы выполнялось хотя бы одно из равенств:
необходимо и достаточно, чтобы выполнялось хотя бы одно из равенств:
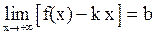 (2)
(2)
или
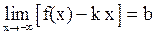 . (3)
. (3)
Если для прямой 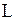 выполняется равенство (2), то она называется правой наклонной асимптотой графика функции
выполняется равенство (2), то она называется правой наклонной асимптотой графика функции 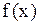 , если (3) – левой наклонной асимптотой.
, если (3) – левой наклонной асимптотой.
Доказательство. Воспользуемся известной из курса аналитической геометрии формулой, дающей расстояние от точки до прямой линии на плоскости.
Следствие. Если прямая линия 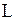 является правой наклонной асимптотой графика функции
является правой наклонной асимптотой графика функции 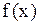 , то выполняется равенство
, то выполняется равенство
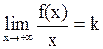 , (4)
, (4)
если – левой наклонной асимптотой, то – равенство
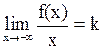 . (5)
. (5)
Доказательство. Пусть, например, прямая 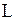 является правой наклонной асимптотой графика функции
является правой наклонной асимптотой графика функции 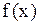 . Тогда из равенства (2) получаем, что
. Тогда из равенства (2) получаем, что
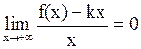 ,
,
то есть
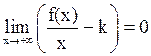 .
.
Следовательно,
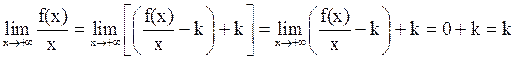 .
.
Равенство (4) доказано.
При решении задач приведённые выше формулы используют в обратном порядке. Сначала для данной функции 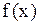 по формулам (4) и (5) находят угловые коэффициенты
по формулам (4) и (5) находят угловые коэффициенты 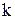 соответствующих наклонных асимптот. Затем, подставляя в формулы (2) и (3) полученные значения
соответствующих наклонных асимптот. Затем, подставляя в формулы (2) и (3) полученные значения 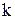 , находят соответствующие коэффициенты
, находят соответствующие коэффициенты 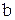 . В результате получается уравнение
. В результате получается уравнение 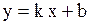 наклонной асимптоты.
наклонной асимптоты.
Если какого-либо из пределов в левых частях формул (5.2)-(5.5) не существует или таковой предел оказывается бесконечным, то соответствующей наклонной асимптоты у графика функции нет.
Наклонную асимптоту 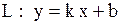 графика функции
графика функции 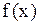 называют горизонтальной, если
называют горизонтальной, если 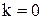 . Таким образом, горизонтальная асимптота имеет уравнение вида
. Таким образом, горизонтальная асимптота имеет уравнение вида 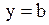 и параллельна оси абсцисс.
и параллельна оси абсцисс.
Дата добавления: 2015-11-18; просмотров: 970;
