Точки перегиба
График функции 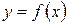 называется выпуклым на интервале
называется выпуклым на интервале 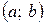 , если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
, если он расположен ниже касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 а).
График функции 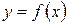 называется вогнутым на интервале
называется вогнутым на интервале 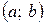 , если он расположен выше касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 б).
, если он расположен выше касательной, проведенной к графику функции в любой точке этого интервала (рис. 8 б).
 | |||
 | |||
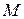
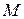
Рис. 8 а Рис. 8 б
| ТЕОРЕМА | (достаточный признак выпуклости (вогнутости) графика функции)
Если 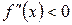 на интервале на интервале 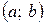 , то график функции является выпуклым на этом интервале; если же , то график функции является выпуклым на этом интервале; если же  , то на интервале , то на интервале 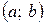 график функции – вогнутый. график функции – вогнутый.
|
Точка кривой, отделяющая ее выпуклую дугу от вогнутой, называется точкой перегиба.
Точки кривой, в которых вторая производная 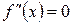 или не существует, называются критическими точками второго рода. Точки перегиба следует искать среди критических точек второго рода.
или не существует, называются критическими точками второго рода. Точки перегиба следует искать среди критических точек второго рода.
В критической точке второго рода 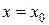 перегиб будет только в том случае, когда при переходе через эту точку
перегиб будет только в том случае, когда при переходе через эту точку 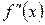 меняет знак.
меняет знак.
Правило. Для определения точек перегиба кривой надо определить все критические точки второго рода и рассмотреть знаки 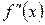 в каждых двух соседних интервалах, на которые эти точки делят область определения функции. В случае, если знаки
в каждых двух соседних интервалах, на которые эти точки делят область определения функции. В случае, если знаки 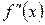 в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах
в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах 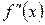 имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
Пример. Определить интервалы выпуклости и вогнутости, точки перегиба графика функции 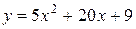 .
.
Решение. Область определения функции – интервал 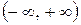 .
.
Найдем первую и вторую производные функции
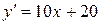 ,
,
 .
.
Так как 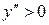 при любом значении
при любом значении  , то кривая вогнута на всем интервале
, то кривая вогнута на всем интервале 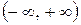 . Точек перегиба нет.
. Точек перегиба нет.
Пример. Определить интервалы выпуклости и вогнутости и точки перегиба графика функции 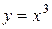 .
.
Решение. Область определения функции – интервал 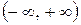 .
.
Найдем первую и вторую производные функции
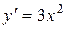 ,
, 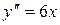 .
.
Решаем уравнение 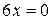 и находим, что
и находим, что 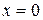 . Это единственная критическая точка. Она делит область определения функции на два интервала
. Это единственная критическая точка. Она делит область определения функции на два интервала 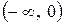 и
и 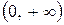 .
.
 |
– +
На интервале 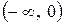 кривая выпукла
кривая выпукла 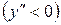 , а на интервале
, а на интервале 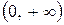 – вогнута
– вогнута 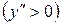 . Таким образом, при переходе через точку
. Таким образом, при переходе через точку 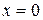 вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты
вторая производная меняет знак. Эта точка является точкой перегиба. Ее координаты 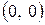 .
.
Дата добавления: 2015-09-28; просмотров: 1613;
