Наклонные асимптоты

Определение.

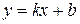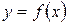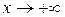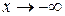Прямая называется наклонной асимптотой графика функции при ( ), если выполняется равенство

.

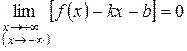Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.

Теорема.

Для того, чтобы график функции 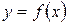имел при 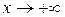( 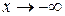) наклонную асимптоту 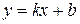, необходимо и достаточно, чтобы существовали конечные пределы

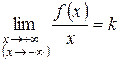и .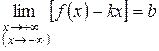

Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая 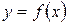наклонной асимптоты не имеет.

Замечания.

1. При отыскании асимптот следует отдельно рассматривать случа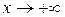и и .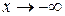

2. Есл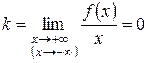и

и ,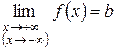

то график функции 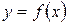имеет горизонтальную асимптоту .

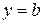3. Есл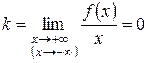и

и ,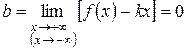

то прямая 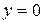(ось Ох) является горизонтальной асимптотой графика функции .

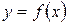Из замечаний следует, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при 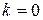. Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:

1) вертикальные асимптоты,

2) наклонные асимптоты.

Пример

Найти асимптоты графика функции .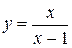

.

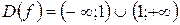1) 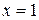− точка разрыва второго рода:

, .

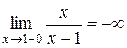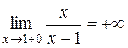Прямая 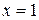− вертикальная асимптота.

2) ,

,

.

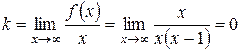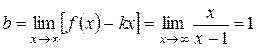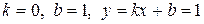Прямая 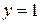− горизонтальная асимптота. Наклонной асимптоты нет.