Распределения времени до отказа
Согласно (2.7), среднее время безотказной работы системы будет равно:
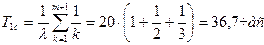
Пример 2.Требуется определить кратность резервирования системы с постоянным резервом, обеспечивающим вероятность безотказной работы 0,96 в течение времени t =150 час. Элементы системы равнонадежны и имеют экспоненциальное распределение со средним временем безотказной работы Т=300 час. Найти также кратность резервирования для системы, элементы которой имеют распределение Рэлея с тем же средним.
Решение: Кратность резервирования может быть определена по формуле:
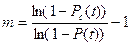
где P(t) – вероятность безотказной работы элемента в течение времени t;
Pc(t)=0,96 – вероятность безотказной работы системы в течение времени t.
Для экспоненциальною распределения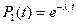 
,где 
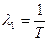интенсивность отказа элемента..
Для распределения Рэлея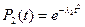 
, где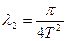 
– параметр распределения.
В течении времени t=150 час получим:
– для экспоненциального закона:
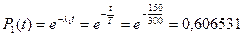
– для закона Рэлея:
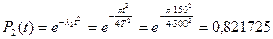
Представляя значения Р1(t) и Р2(t) в формулах для кратности резервирования m, получим:
– для экспоненциального распределения:
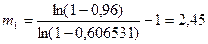
– для распределения Рэлея:
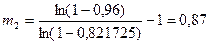
Округляя до целых чисел в большую сторону, получим m1=3, m2=1. Таким образом, для достижения заданной надежности в первом случае потребуется 3 резервных элемента, а во втором случае – только один.
Из примера видно, что надежность системы определяется не только ее структурой и временем работы, но также законом распределения времени до отказа элементов.
Пример 3. В условиях предыдущего примера необходимо обеспечить заданную надежность системы в течении времени t=450 час.
Решение: определим вероятность безотказной работы элемента в течение времени t=450 час для экспоненциального распределения и распределения Рэлея:
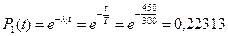
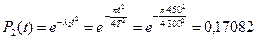
Найдем кратность резервирования:
– для экспоненциального распределения:
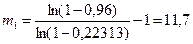
– для распределения Рэлея:
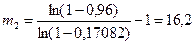
Округление до целых чисел дает требуемую кратность m1=12, m2=17.Если система работает время t =450 час, то для достижения заданной надежности необходимо иметь 12резервных элементов в первом случае и 17 резервных элементов во втором случае.
Из расчета следует, что структурное резервирование не может обеспечить вероятность безотказной работы системы 0,96 в течение 450 часов. Кратность резервирования настолько высока, что ее практическая реализуемость вряд ли возможна.
Пример 4.Дана резервированная система с постоянным резервом кратности m, все элементы которой равнонадежны и имеют усеченный нормальный закон распределения времени до отказа с параметрами m0 = 400 час и σ0 = 200 час.
Определить все показатели надежности системы. Результаты представить в виде таблиц и графиков. Принять m = 0,1,2.
Решение: для равнонадежных элементов формулы (1)–(3) показателей надежности принимают вид:
Pc(t) = 1– (1–P(t))m+1
fc (t)=(m+1)f(t)(1–P(t)) m
λс(t) =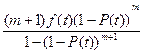 
Плотность распределения времени до отказа и вероятность безотказной работы для усеченного нормального распределения равны соответственно:
f(t) =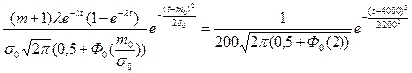 
P(t) =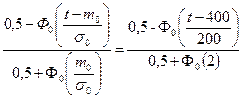 
где Ф0 (t) – функция Лапласа.
Значения вероятности безотказной работы системы Pc(t) для кратности резервирования m = 0,1,2 содержатся в табл. 2. Соответствующие графики приведены на рис. 4.
Таблица 2
Дата добавления: 2015-09-07; просмотров: 1801;