При различной кратности резервирования
Следует иметь в виду, что при больших значениях t вероятность безотказной работы настолько мала, что нет смысла эксплуатировать систему. Таблица необходима только для иллюстрации результатов решения задачи, представления решения в графическом виде и вычисления среднего времени безотказной работы системы методом Симпсона.
Из графиков следует, что Pc(t) возрастает при увеличении кратности резервирования, причем этот эффект тем сильнее, чем меньше m.
На основе данных таблицы 2 приближенно вычислим среднее время безотказной работы системы для значений m = 0,1,2. Воспользуемся формулой Симпсона:
Т1 = 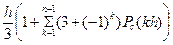
в которой шаг интегрирования примем равным h = 50 час, n = 20. Расчеты показывают, что при m= 0 Т1 ≈ 411 час, при m = 1 Т1 ≈ 518 час, при m = 2 T1≈573 час.
В табл. 3 содержатся значения плотности распределения вероятностей fc(t) для той же кратности и резервирования. Графики fc(t) приведены на рис. 5.
Таблица 3
Дата добавления: 2015-09-07; просмотров: 1051;
