Порядок выполнения работы. 1. Внимательно изучите теоретические положения и примеры расчетов.
1. Внимательно изучите теоретические положения и примеры расчетов.
2. Выполните расчеты по заданиям, приведенным ниже.
3. Подготовьте отчет.
Задание.1. Техническая система представляет собой дублированную систему с постоянно включенным резервом. Вероятность безотказной работы основной и резервной подсистем в течение t = 200 час равна 0,8. Найти вероятность безотказной работы и вероятность отказа системы в течение времени t. Найти среднее время безотказной работы системы при условии, что ее подсистемы имеют постоянную интенсивность отказа.
Задание 2.Интенсивность отказа элементов системы λ=0,0025 час-1. Требуется определить кратность резервирования системы с постоянно включенным резервом, построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы Тl c=800 час.
Задание 3.Найти показатели надежности резервированной системы с постоянным резервом кратности m=3, элементы которой имеют интенсивности отказа λ0 = 0,004 час 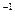 ,
, 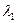 = 0,007 час
= 0,007 час 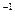 ,
, 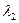 =0,002 час
=0,002 час 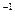 ,
, 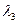 =0,001 час
=0,001 час 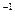 . Время непрерывной работы системы t = 120 час.
. Время непрерывной работы системы t = 120 час.
Задание 4. Определить показатели надежности мажоритарной системы, состоящей из 6 равнонадежных элементов, время до отказа которых равномерно распределено на интервале от 0 до 1000 часов. Количество резервных элементов равно 2. Получить аналитическое и графическое представления показателей надежности системы.
Задание 5. Получить формулу для вероятности безотказной работы мажоритарной системы, состоящей из элементов разной надежности при n = 4, m = 2.
Задание 6.Интенсивность отказа одного элемента λ = 0,0035 час 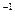 . Требуется определить кратность резервирования системы (резерв замещением), построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы T
. Требуется определить кратность резервирования системы (резерв замещением), построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы T 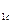 =800 час.
=800 час.
Задание 7.Найти показатели надежности P 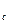 (t), Тс,
(t), Тс, 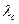 (t) резервированной системы (резерв замещением) кратности m =3, элементы которой имеют интенсивности отказа λ
(t) резервированной системы (резерв замещением) кратности m =3, элементы которой имеют интенсивности отказа λ 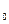 =0,04 час
=0,04 час 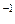 , λ
, λ 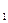 = 0,07час
= 0,07час 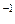 , λ
, λ 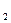 = 0,02 час
= 0,02 час 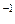 , λ
, λ 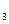 = 0,1 час
= 0,1 час 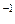 . Решение получить в виде формул, таблиц и графиков.
. Решение получить в виде формул, таблиц и графиков.
Задание 8. Для резерва замещением кратности m получить формулу вероятности безотказной работы, если элементы системы равнонадежны и имеют гамма-распределение времени до отказа с параметрами 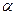 и
и 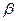 .
.
Задание 9. Для резерва замещением кратности m получить формулу плотности распределения времени безотказной работы при условии, что системы равнонадежны и имеют нормальное распределение с параметрами m и 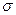 (
( 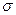 <m/3).
<m/3).
Задание 10. Даны две системы со скользящим резервом. Первая система состоит из n = 7 элементов, из которых m=3 резервных. Вторая система состоит из n= 5 элементов с m = 2 резервными. Определить более надежную систему по критерию вероятности безотказной работы. Элементы обеих систем имеют постоянную интенсивность отказа λ =0,01 час 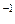 .
.
Задание 11. Дана последовательно-параллельная система размером 3×5 (5 элементов нерезервированной системы, 3 резервных подсистемы) с постоянно включенным резервом. Все элементы имеют одинаковую надежность, время до отказа элементов имеет распределение Рэлея с математическим ожиданием Т = 50 час. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию Pc(t). Указание: воспользоваться формулами (8) и (14).
Задание 12. Дана последовательно-параллельная система размером 3×5 (5 элементов нерезервированной системы, 3 резервных подсистемы), резервированная методом замещения. Все элементы имеют одинаковую интенсивность отказа λ=0,02 час 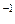 . Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию Pc(t). Указание: воспользоваться формулами (9) и (15).
. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию Pc(t). Указание: воспользоваться формулами (9) и (15).
Задание 13. Элементы резервированной системы с постоянно включенным резервом имеют распределение Вейбулла времени работы до отказа. Найти выражениедля среднего времени безотказной работы системы при кратности резервирования m = 0,1, 2, 3,4, 5. Вычислить среднее время безотказной работы при параметрах закона распределения 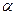 =2,5,
=2,5, 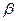 = 20. Решение представить в виде таблицы.
= 20. Решение представить в виде таблицы.
Задание 14. Даны две системы с постоянно включенным резервом с дробной кратностью резервирования m = 1/2 и m = 2/3 соответственно. Определить показатели надежности систем Pc(t), Tc, λc(t). Решение представить в виде формул, графиков и таблиц. Известны следующие исходные данные для числового анализа: время работы системы t= 0÷500 час, среднее время безотказной работы нерезервированной системы Т=550 час, основная и все резервные системы равнонадежны и имеют экспоненциальное распределение времени до отказа.. Определить какая из систем имеет более высокие показатели надежности.
Задание 15.Даны две системы, описанные в задание 14. Определить критическое время t 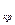 , свыше которого резервирование с дробной кратностью не целесообразно. Определить значение вероятности Р(tкр). Решение получить в аналитическом и численном виде.
, свыше которого резервирование с дробной кратностью не целесообразно. Определить значение вероятности Р(tкр). Решение получить в аналитическом и численном виде.
Задание 16. Резервированная система с постоянно включенным резервом состоит из двух подсистем, имеющих различные законы распределения времени до отказа. Необходимо вычислить Рс(t), T 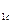 , λ
, λ 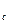 (t). Решение получить в аналитическом виде, в виде графиков и таблиц. Графики представить в диапазоне t = 0÷500 час. Исходные данные содержатся в табл. 6.
(t). Решение получить в аналитическом виде, в виде графиков и таблиц. Графики представить в диапазоне t = 0÷500 час. Исходные данные содержатся в табл. 6.
Таблица 6
Дата добавления: 2015-09-07; просмотров: 2735;
