Сводные данные расчетных значений статистических характеристик

Последовательность расчетов статистических характеристик:

Составить ряд распределения.

Для упрощения расчета численных значений случайной величины разбиваются на несколько интервалов. При объеме выборки около 100 единиц рекомендуется назначать 6–10 интервалов. Ширина интервала равна

∆X=W/k, (1)

где W = Х_тax – X_mjn –размах выборки;

Х_тах Х_mjn –максимальное и минимальное значения случайной величины в выборке;

к –число интервалов.

В колонку 2 табл. 1 записываются границы интервалов в порядке воз­растания случайной величины. т. е. составляется ряд распределения.

1.2. Рассчитать среднее значение выборки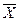

Для этого в каждом интервале определяется среднее значение интерва­ла, подсчитывается частота n_i попадания случайных величин в каждый ин­тервал. При этом если значение попадает вне границы двух интервалов, его нужно отнести к левому интервалу.

Среднее значение выборки определяется по формуле

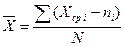(2)

где X_{cp i} – середина i-го интервала;

n_i–число случаев в i-том интервале;

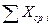–сумма значений по вертикали в колонке 5;

N –объем выборки;

к –число интервалов.

Среднее число выборки и является средней наработкой на отказ Т₀.

1.3. Определить дисперсию выборки Д и среднее квадратическое от­клонение σ.

Дисперсия случайной величины характеризует ее рассеивание около математического ожидания. Для выборки объемом N дисперсия определя­ется по формуле

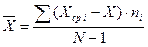(3)

В соответствии c этой формулой для каждого интервала рассчитываетcя разность и заполняются последовательно колонки 6, 7 и 8 табл. 1. Числитель формулы 2 является суммой всех значений в колонке 8.

Среднее квадратическое отклонение равно корню квадратному из дисперсии,

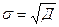(4)

Размерность среднего квадратического отклонения совпадает с размерностью случайной величины.

1.4. Рассчитать коэффициент вариации. Числовое значение коэффициента вариации

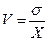. (5)

2. Определить закон распределения наработки между отказами

Закон распределения характеризует связь между значениями случайной величины и соответствующими им вероятностями. Случайные величины, используемые для оценки показателей надежности, наиболее часто подчиня­ются нормальному, экспоненциальному или распределению Вейбулла.

2.1. Построить гистограмму эмпирического распределения и выдви­нуть статистическую, гипотезу.

Гистограмма распределения строится по результатам расчета статистической вероятности. Статистической вероятностью является частность

P_i = n_i /N, (6)

где n_i – число случаев в i-ом интервале;

N – объем выборки.

Значение Р необходимо записать в колонку 9 табл. 1.

При построении гистограммы по оси абсцисс откладываются интерва­лы (берутся из табл. 1) и на каждом интервале строятся прямоугольники, высота которых равна Р. Масштаб по оси ординат выбирается в зависимо­сти и от максимального значения Р.

По виду гистограммы необходимо выдвинуть статистическую гипоте­зу, т. е. предварительно определить закон распределения случайной величи­ны. При этом учесть, что если коэффициент вариации V<0,33, то наиболее вероятно нормальное распределение; если К=0,33–2,00, то может быть рас­пределение Вейбулла; если V =1,0, вероятным является экспоненциальное распределение.

2.2. Проверить статистическую гипотезу.

Правдоподобие гипотезы оценивается критериями согласия. С помо­щью критериев определяется – с какой вероятностью эмпирическое распре­деление согласуется с теоретическим, т. е. оценивается сходимостью по ве­роятности.

Наиболее часто применяется критерий Пирсона, который рассчитыва­ется по формуле

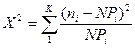(7)

где к, п_i, N –см. уравнение 1 и табл. 1;

P_i – теоретическая вероятность в каждом интервале.

Предварительный анализ информации показывает, что распределение между отказами машин во всех вариантах задания близко к экспонентному. В связи с этим в данной работе предлагается оценить сходимость с экспо­ненциальным законом.

Таблица 2