Теоретические положения. Критериинадежности резервированных невосстанавливаемых систем те же, что инерезервированных невосстанавливаемых систем.
Критериинадежности резервированных невосстанавливаемых систем те же, что инерезервированных невосстанавливаемых систем.
Основными видами резервирования являются: общее постоянное, общее замещением,раздельноепостоянное, раздельное замещением. Структурные схемы резервированных систем приведены на рис. 1.
Приведемосновные соотношения для показателей надежности резервированных систем.
1. Общее резервированиес постоянно включенным резервом
Пусть Pi (t) – вероятность безотказной работы i-го элемента за время t, Qi(t) – вероятность отказа i-го элемента за время t, fi (t) – плотность распределения времени до, отказа i-го элемента в момент времени t. Тогда вероятность безотказной работы, плотностьраспределения времени безотказной работы и интенсивность отказов системы с кратностьюрезервирования m определяются соотношениями:
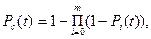 (1)
(1)
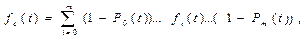 (2)
(2)
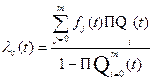 (3)
(3)
В частности, для экспоненциальных распределений времени до отказа элементов с одинаковыми параметрами λ имеют место равенства:
P(t) = 1–(1 – eλt)m+1 (4)
ƒ(t) = (m + 1) λe-λt(1 – eλt)m (5)
λc(t) = 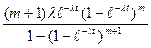 (6)
(6)
Среднее времябезотказной работы системы определяется выражением:
Т1 = 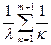 (7)
(7)



Рис. 1. Структурные схемы резервированных систем: а – общее резервирование с постоянно включенным резервом; б – раздельное резервирование с постоянно включенным резервом; в – общее резервирование замещением; г – раздельное резервирование замещением
Формулы справедливы для случая, когда нерезервированная система рассматривается как один элемент, показатели надежности которого известны. В действительности любая система состоит из большого числа элементов, каждый из которых имеет показатель надежности, самостоятельно учитываемый при расчете. В таком случае формула для вероятности безотказной работы имеет вид:
Pс(t) = 1– 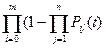 (8)
(8)
где n – число элементов нерезервированной системы;
Рij(t) – вероятность безотказной работы элемента с номером (i,j).
2. Общее резервирование замещением
Вероятность безотказной работы, плотность распределения времени до отказа и среднее время безотказной работы системы определяются выражениями:
Pс (t)= P0 (t)+ 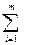 ƒ0 · ƒ1 · … · ƒi=1· Pi(t) (9)
ƒ0 · ƒ1 · … · ƒi=1· Pi(t) (9)
ƒс(t)= ƒо · ƒ1 · … ·ƒm (t)(10)
Т1 = 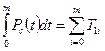 (11)
(11)
Если все элементы равнонадежны, то
Pс (t)= 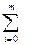 ƒ*(i) · P(t) = 1 -
ƒ*(i) · P(t) = 1 - 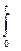 f*(m+1)(
f*(m+1)( 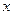 )dx (12)
)dx (12)
Формулы содержат свертки функций, обозначенные символом (*). Свертка функций f(t) и g(t), заданных при t 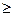 0. определяемся соотношением:
0. определяемся соотношением:
f * g(t) = 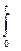 f(t - x)g(x)dx =
f(t - x)g(x)dx = 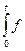 (x)g(t – x)dx
(x)g(t – x)dx
Выражение ƒ*(i) (t) = f * f * …* f(t) представляет собой i-кратную свертку функций f(t).
Если интенсивность отказов элементов постоянна и равна λ, то формулы для вероятности и среднего времени безотказной работы системы имеют вид:
Pс(t) = 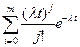 (13)
(13)
Tc = 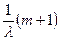
3. Раздельное резервирование
Пусть исходная система состоит из n элементов. Тогда вероятность безотказной работы системы при раздельном резервировании выражается следующими формулами:
– раздельное резервирование с постоянно включенным резервом:
Pс(t) = 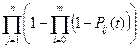
 (14)
(14)
– раздельное резервирование замещением:
Pс(t) = 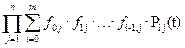 (15)
(15)
В формулах приняты следующие обозначения: 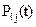 – вероятность безотказной работы элемента с номером (i, j), fij(t) плотность распределения времени до отказа элемента, i=0,1,2, ..., m; j=1,2, ...., n.
– вероятность безотказной работы элемента с номером (i, j), fij(t) плотность распределения времени до отказа элемента, i=0,1,2, ..., m; j=1,2, ...., n.
4. Резервирование с дробной кратностью
Приведем формулы для показателей надежности мажоритарных систем (систем с дробной кратностью резервирования), в которых n – общее число элементов, (n-m) основных и m резервных элементов. Отказ такой системы наступает при отказе (m+1)-го элемента.
Показатели надежности мажоритарной системы при условии, что все элементы имеют одинаковую надежность, вычисляются по формулам:
Pc(t) = 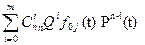 (16)
(16)
ƒc(t) = (n – т)С 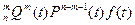 (17)
(17)
λc(t)= 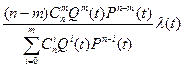 (18)
(18)
5. Скользящее резервирование
Скользящее резервирование представляет собой резервирование замещением с кратностью m/(n-m), где n – общее число элементов, m - число резервных элементов, (n-m) – число оcновных резервируемых элементов.
Вероятность безотказной работы системы со скользящим резервом при условии, что все элементы системы имеют одинаковую надежность, равна
Pc(t) = 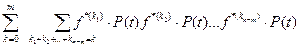 (19)
(19)
Если элементы системы имеют экспоненциальное распределение вероятностей временидо отказа с параметром λ, то вероятность безотказной работы, интенсивностьотказов и среднее время безотказной работы системы соответственно равны:
Pc(t) = 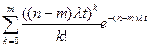 (20)
(20)
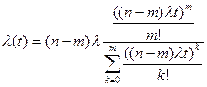 (21)
(21)
T1c= 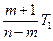 (22)
(22)
Дата добавления: 2015-09-07; просмотров: 1610;
