Интегрирование по частям.
Пусть u(x) и v(x)- дифференцируемые функции, Тогда справедлива формула интегрирования по частям: 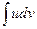 =uv-
=uv- 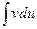 .
.
Указанная формула позволяет свести вычисление интеграла 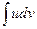 к вычислению интеграла
к вычислению интеграла 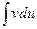 . Если принято решение об интегрировании по частям то это целесообразно производить следующим образом:
. Если принято решение об интегрировании по частям то это целесообразно производить следующим образом:
1) подынтегральное выражение содержит в виде сомножителя функции lnx, arcsinx, arccosx, arctgx. В качестве u(x) выбирают указанные функции;
2) подынтегральная функция имеет вид P(x) 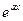 , P(x)sin ax, P(x)cos ax, где P(x)- многочлен относительно переменной x.
, P(x)sin ax, P(x)cos ax, где P(x)- многочлен относительно переменной x.
В качестве u(x) выбирают P(x).
3) подынтегральная функция имеет вид 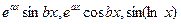 и т.д. После двукратного применения формулы интегрирования по частям получаем исходный интеграл с некоторым коэффициентом. Решая уравнение находим искомый интеграл.
и т.д. После двукратного применения формулы интегрирования по частям получаем исходный интеграл с некоторым коэффициентом. Решая уравнение находим искомый интеграл.
Примеры.
1) 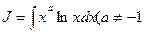 ). Полагаем u=lnx, dv=xadx, тогда du=dlnx=(lnx)’dx=
). Полагаем u=lnx, dv=xadx, тогда du=dlnx=(lnx)’dx= 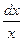 ,
, 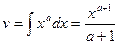
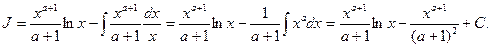 2)
2) 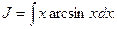 Полагаем u=arcsinx, dv=xdx, тогда
Полагаем u=arcsinx, dv=xdx, тогда 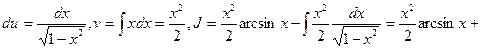
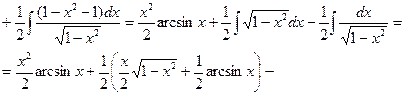
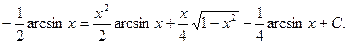
3) 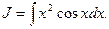 Полагаем
Полагаем 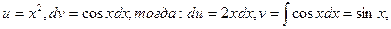
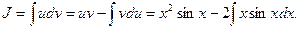
Для вычисления 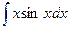 полагаем
полагаем 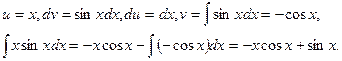
Таким образом 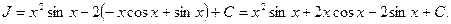
4) 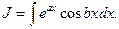
Полагаем 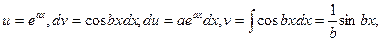
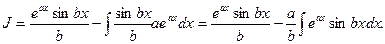
Чтобы вычислить 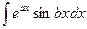 полагаем
полагаем
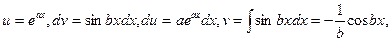
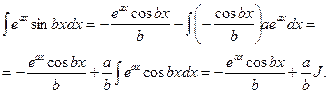
Далее 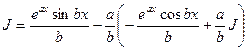 или
или
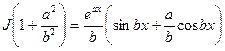 .
.
Дата добавления: 2015-10-13; просмотров: 725;
