Свойства определенного интеграла. Предполагаем, что все рассматриваемые ниже функции непрерывны на сегменте .
Предполагаем, что все рассматриваемые ниже функции непрерывны на сегменте 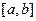 .
.
а) Интеграл от суммы(разности) функций 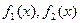 равен суме(разности) интегралов от этих функций:
равен суме(разности) интегралов от этих функций: 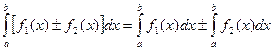 ;
;
б) постоянная выносится за знак интеграла: 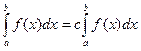
в) определённый интеграл с равными нижним и верхним пределами равен нулю: 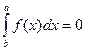 ;
;
г) при перестановке пределов интегрирования, знак определённого интеграла меняется на противоположный: 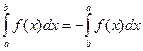
г) для любых a,b,c справедливо 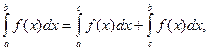
д) если 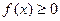 на
на 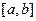 , то
, то 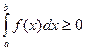 ,
,
е) если 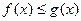 на
на 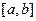 , то
, то 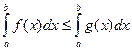 ,
,
ж) 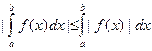 ,
,
г) найдется такая точка 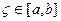 , что
, что
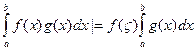 .
.
Следствие . При 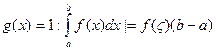
Пусть 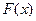 - любая первообразная функции
- любая первообразная функции 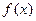 . Тогда имеет место формула Ньютона-Лейбница
. Тогда имеет место формула Ньютона-Лейбница 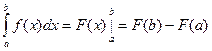 Замена переменной в определенном интеграле: пусть функция
Замена переменной в определенном интеграле: пусть функция 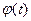 непрерывна на
непрерывна на 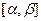 , а функция
, а функция 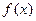 непрерывна вместе со своей производной на
непрерывна вместе со своей производной на 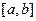 , причем
, причем 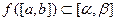 , тогда справедлива формула:
, тогда справедлива формула:
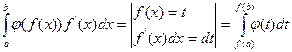 .
.
Пусть 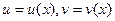 - непрерывно дифференцируемые на
- непрерывно дифференцируемые на 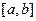 функции. Формула интегрирования по частям имеет вид:
функции. Формула интегрирования по частям имеет вид: 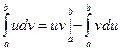
Примеры.
1. 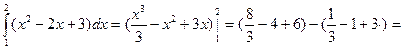
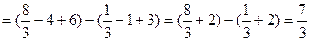 ;
;
2. 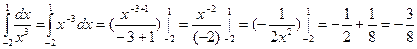 ;
;
3. 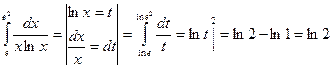 ;
;
4. 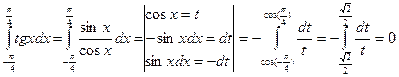 ;
;
5. 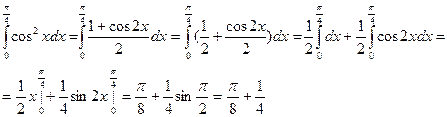
6. 
= 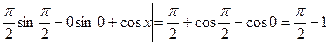 ;
;
7. 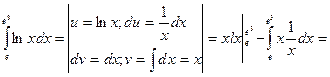
= 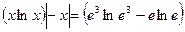
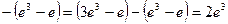 ;
;
8. 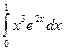 ; находим первообразную:
; находим первообразную:
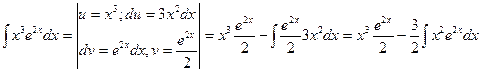 вычислим
вычислим
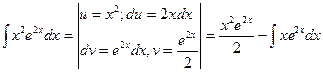 ,
,
вычислим 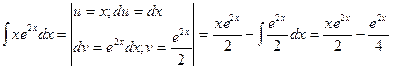
Подставим найденные первообразные и вычислим
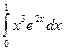 =
= 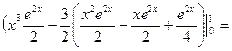
= 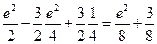 .
.
Дата добавления: 2015-10-13; просмотров: 632;
