Интегрирование подведением под знак дифференциала.
Для использования метода запишем таблицу дифференциалов, которая легко получается из таблицы производных и таблицы интегралов. В первом случае применяем формулы для дифференциалов функции, записанных в обратном порядке, во втором – путем взятия знака дифференциала от обеих частей равенства. Таблица дифференциалов.
1. 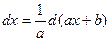 8.
8. 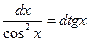
2. 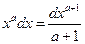 9.
9. 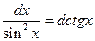
3. 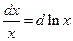 10.
10. 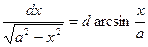
4. 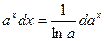 11
11 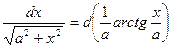
5. 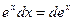 12.
12. 
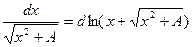
6. 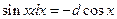 13.
13. 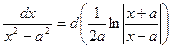
7. 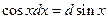
Примечание.
Формулы для дифференциалов функции 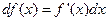 не меняются от того является ли x независимой переменной или есть некоторая функция u(t) другой независимой переменной t. (свойства инвариантности формы первого дифференциала )
не меняются от того является ли x независимой переменной или есть некоторая функция u(t) другой независимой переменной t. (свойства инвариантности формы первого дифференциала )
Поэтому таблица дифференциалов будет иметь место, если вместо x подставить u(t). C помощью формулы для дифференциала функции записанной в обратном порядке 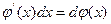
некоторые интегралы 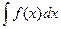 могут быть сведены к виду
могут быть сведены к виду
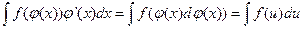 , которые легко сводятся к табличным. Здесь
, которые легко сводятся к табличным. Здесь 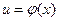 .
.
Указанное преобразование называется «Подведение под знак дифференциала».
Примеры. 1) 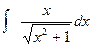 =
= 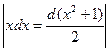 = =
= = 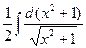 =
=
= 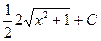 =
= 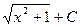
2) 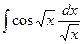 =
= 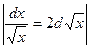 =
= 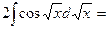
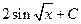 .
.
3) 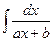 =
= 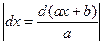 =
= 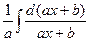 =
= 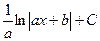
4) 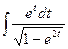 =
= 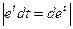 =
= 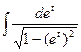 =arcsin(
=arcsin( 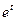 )+C
)+C
5) 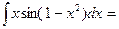
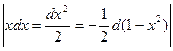 =
=
= 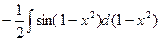 =
= 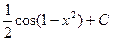
2. Метод подстановки.
Иногда удается подобрать в качестве новой переменной такую дифференцируемую функцию 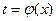 , что имеет место равенство f(x)dx = q(
, что имеет место равенство f(x)dx = q( 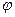 (x))
(x)) 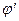 (x)dx, причем интеграл
(x)dx, причем интеграл 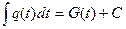 легко вычисляется. Таким образом:
легко вычисляется. Таким образом:
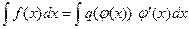 =
= 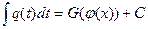
Указанный прием вычисления интеграла 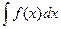 называется интегрирование методом замены переменной.
называется интегрирование методом замены переменной.
Примеры.
1) 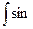 (6x-5)dx. Подстановка
(6x-5)dx. Подстановка 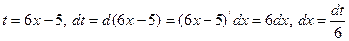
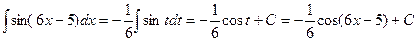
2) 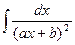 ; подстановка t=ax+b,
; подстановка t=ax+b,
тогда dt=d(ax+b)=(ax+b 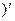 dx=adx, dx=
dx=adx, dx= 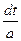 ,
,
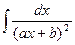 =
= 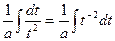 =
= 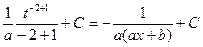
3) 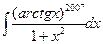 .
.
Подстановка 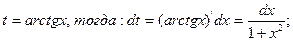
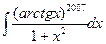 =
= 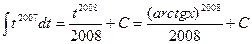
4) 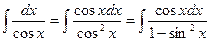 ; подстановка
; подстановка
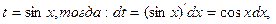
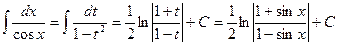
5) 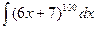 ; подстановка
; подстановка 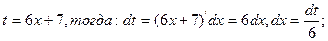
Дата добавления: 2015-10-13; просмотров: 1129;
