Частные производные. Градиент.
Определение. Частной производной первого порядка функции двух переменных 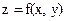
по переменной х называется производная по х при условии, что переменная у является постоянной. Обозначается 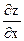 . Точно также определяется частная производная по переменной у. Обозначается
. Точно также определяется частная производная по переменной у. Обозначается 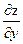 . При этом постоянной будет х.
. При этом постоянной будет х.
Пример. 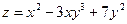 . Найти частные производные первого порядка.
. Найти частные производные первого порядка.
Решение. 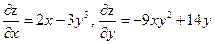 .
.
Определение. Частной производной 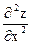 второго порядка функции двух переменных
второго порядка функции двух переменных 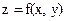 называется производная по х частной производной первого порядка
называется производная по х частной производной первого порядка 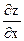 при условии, что переменная у является постоянной. Находится по формуле
при условии, что переменная у является постоянной. Находится по формуле
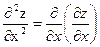
Аналогично определяется частная производная 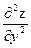 :
:
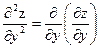 . Здесь х постоянна.
. Здесь х постоянна.
Смешанная частная производная второго порядка 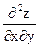 определяется по формуле:
определяется по формуле:
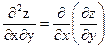 или
или 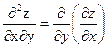
Пример. Найти смешанную частную производную второго порядка 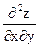 , если
, если
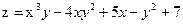 .
.
Решение. 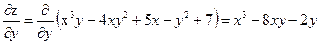 ,
,
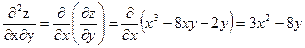 .
.
Ответ. 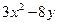 .
.
Определение. Частной производной первого порядка по одной из переменной 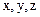 функции
функции 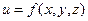 называется производная по этой переменной, при условии, что две другие остаются постоянными. Обозначаются
называется производная по этой переменной, при условии, что две другие остаются постоянными. Обозначаются 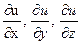 .
.
Пример. 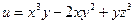 . Найти частные производные первого порядка.
. Найти частные производные первого порядка.
Решение. 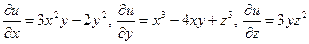
Определение. Градиентом скалярного поля 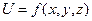 в точке
в точке 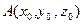 называется вектор
называется вектор 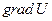 , определяемый по правилу
, определяемый по правилу 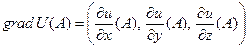 .
.
Дата добавления: 2015-10-13; просмотров: 973;
