Первообразная. Неопределенный интеграл.
Определение. Функция F(х) называется первообразной для функции f(х) на промежутке Х, если в любой точке х этого промежутка выполняется равенство F′(х)= ƒ(х)
Примеры.
1) Функция F(х)=tg х является первообразной для функции
ƒ(х)= 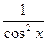 на интервале (-
на интервале (- 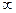 ,+
,+ 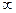 ,) х ≠
,) х ≠ 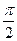 +π n,
+π n,
так как 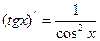
2) Функция F(х) = 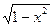 является первообразной для функции
является первообразной для функции
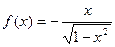 на интервале (-1,1), так как
на интервале (-1,1), так как 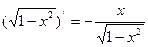
3) Функция F(х)=lnx является первообразной для функции ƒ(х)= 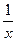 на интервале (0,+
на интервале (0,+ 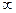 ), так как (lnх)َ =
), так как (lnх)َ = 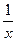
Определение. Совокупность всех первообразных для функции f(х) называется неопределенным интегралом от функции f(х) на Х и обозначается 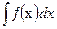 .
.
Здесь знак 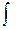 называется знаком интеграла, выражение f(x)dx – подынтегральным выражением, а f(x) – подынтегральной функцией. Если F(х) – одна из первообразных для f(х) на Х, то
называется знаком интеграла, выражение f(x)dx – подынтегральным выражением, а f(x) – подынтегральной функцией. Если F(х) – одна из первообразных для f(х) на Х, то 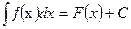 , где С- произвольная постоянная.
, где С- произвольная постоянная.
Примеры.
1) 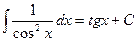 , так как функция F(х)=tgx – одна из первообразных для
, так как функция F(х)=tgx – одна из первообразных для 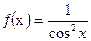 на Х .
на Х .
2) 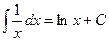 на интервале (
на интервале ( 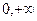 ), так как функция F(x)=ln x одна из первообразных для ƒ
), так как функция F(x)=ln x одна из первообразных для ƒ 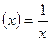 на этом интервале.
на этом интервале.
Основные свойства неопределенного интеграла.
1.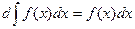 ,2.
,2. 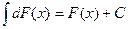 ,
,
3. 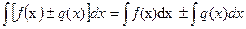 ,
,
4. 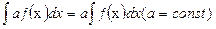
Таблица интегралов.
1. 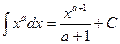
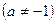 , в частности,
, в частности,
1.1 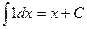 , 1.2
, 1.2 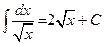 ; 2.
; 2. 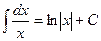 , 3.
, 3. 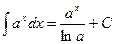 , 4.
, 4. 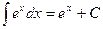 ,
,
5. 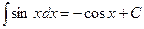
 , 6.
, 6. 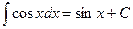 ,
,
7. 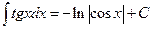 , 8.
, 8. 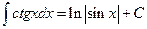 ,
,
9. 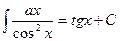 , 10.
, 10. 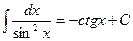 ,
,
11 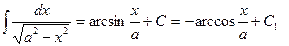 ,
,
12. 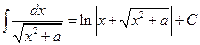 ,
,
13. 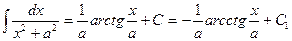 ,
,
14. 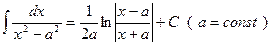 ,
,
15. 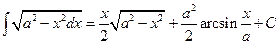 , 16.
, 16. 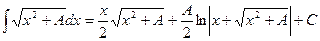 .
.
Примеры.
1) 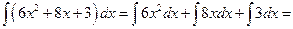 =
= 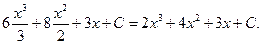
Здесь 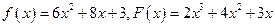 .
.
Проверка. 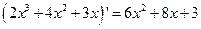 2. 2)
2. 2) 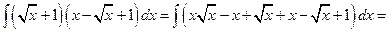
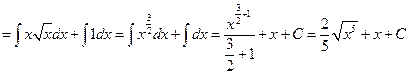 .
.
Проверка. 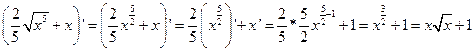 3)
3) 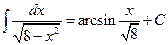 , используется табличный интеграл , здесь
, используется табличный интеграл , здесь 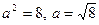 ,
,
4) 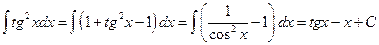 .
.
Проверка. 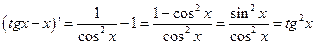 .
.
5) 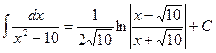 , используется табличный интеграл, здесь a2 =10, тогда a=
, используется табличный интеграл, здесь a2 =10, тогда a= 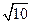 .
.
Дата добавления: 2015-10-13; просмотров: 872;
