Неопределенный интеграл

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Первообразная функция

Основной задачей дифференциального исчисления является нахождение производной от данной функции. Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную 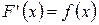. Искомую функцию называют первообразной функции .

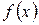Определение.

Функция 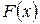называется первообразной функции 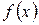на интервале 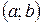, если для любого 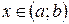выполняется равенство:

.

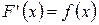Примеры

1. Функция 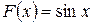является первообразной для функции 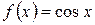при любом х, так как .

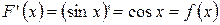2. Функция 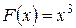есть первообразная для функции 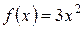на всей числовой оси, ибо .

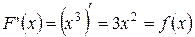Нетрудно заметить, что любая функция вида 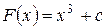, где с − постоянная, также является первообразной для функции 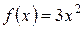, поскольку .

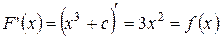Приведем теорему, выражающую основное свойство первообразной.

Теорема.

Если функция 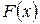является первообразной функции 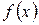на интервале 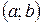, то множество всех первообразных для 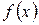задается формулой

,

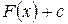где с − постоянное число.

Таким образом, множество функций 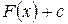представляет собой семейство всех первообразных для данной функции .

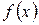Неопределенный интеграл

Определение.

Совокупность всех первообразных функций 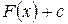для данной функции 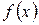на интервале 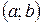называется неопределенным интегралом.

Обозначается:

,

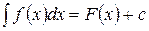где 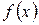− подынтегральная функция,

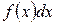− подынтегральное выражение.

Операция нахождения первообразной для данной функции называется интегрированием этой функции.

Дифференцирование и интегрирование функций − это две взаимно обратные операции.

Определение.

График какой-либо первообразной 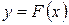функции 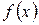называется интегральной кривой.

Геометрически неопределенный интеграл представляет собой семейство параллельных кривых 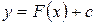, в котором каждому числовому значению с соответствует определенная кривая (рис.6.1).

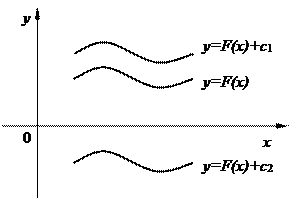Рис. 6.1

Условие существования первообразной или неопределенного интеграла сформулировано в следующей теореме.

Теорема.

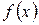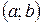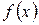Если функция непрерывна на интервале , то имеет на этом интервале первообразную, а следовательно, и неопределенный интеграл.

Замечание.

Если функция 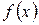имеет точки разрыва, то ее можно интегрировать на каждом промежутке непрерывности раздельно.