Вычисление криволинейного интеграла первого рода

1) Кривая L задана параметрически: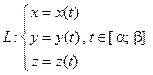

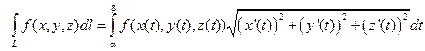
2) Линия L задана на плоскости XOY явно, т.е. L: y = y(x), . Тогда

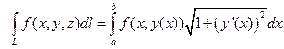
3) Линия L задана на плоскости в полярных координатах: ,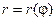

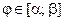
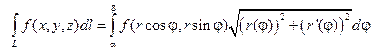
Геометрические и физические приложения криволинейного интеграла первого рода:

1) длина дуги кривой ;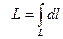

2) площадь цилиндрической поверхности (Рис.2)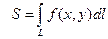

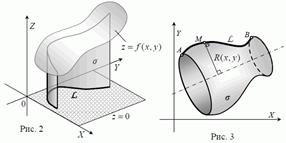
3) площадь поверхности вращения (Рис.3) ;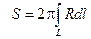

4) масса материальной линии плотности μ: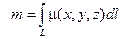

5) координаты центра масс.