Вычисление площадей плоских фигур с помощью определенного интеграла

Пример 1. Найти площадь фигуры, ограниченной линиями у = х² – 2 и y = x.

График функции y= х² – 2 представляет собой параболу с точкой минимума при x = 0, y = -2; ось абсцисс пересекается в точках 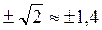. График функции у = х – прямая, биссектриса неотрицательной координатной четверти.

Найдем координаты точек пересечения параболы у = х² – 2 и прямой у = х, решив систему этих уравнений:

х² – 2 = х

х² – х - 2 = 0

Д = 1 + 8 = 9

х = 2; y = 2 или х = -1; y = -1

Таким образом, фигуру, площадь которой необходимо найти, можно представить на рисунке 4.9.

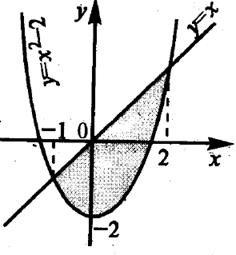
Рисунок 4.9 – Фигура, ограниченная линиями у = х² – 2 и y = x

На отрезке [-1, 2] х ≥ х² – 2 .

Воспользуемся формулой 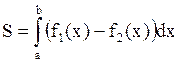, полагая f₁(х) = х; f₂(х) = х² – 2; a = -1; b = 2.

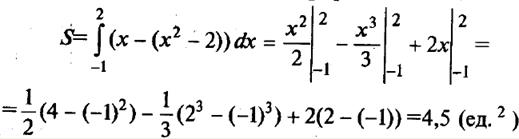
Пример 2. Найти площадь фигуры, ограниченной линиями у = 4 - х² и y = х² – 2x.

График функции y = 4 - х² представляет собой параболу с точкой максимума при x = 0, y = 4; ось абсцисс пересекается в точках 2 и -2. График
функции у = х² – 2x – парабола с точкой минимума при 2x - 2 = 0, х = 1; y = -1; ось абсцисс пересекается в точках 0 и 2.

Найдем координаты точек пересечения кривых:

4 - х² = х² – 2х

2х² – 2х - 4 = 0

х² – х - 2 = 0

Д = 1 + 8 = 9

х = 2; y = 0 или х = -1; y = 3

Таким образом, фигуру, площадь которой необходимо найти, можно предствить на рисунке 4.10.

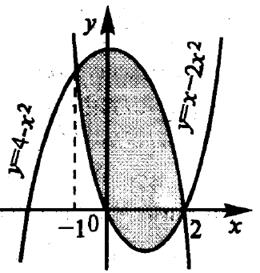
Рисунок 4.10 - Фигура, ограниченная линиями у = 4 - х² и y = х² – 2x

На отрезке [-1, 2] 4 - х² ≥ х² – 2x.

Воспользуемся формулой 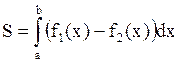, полагая f₁(х) = 4 -
- х²; f₂(х) = х² – 2х; a = -1; b = 2.

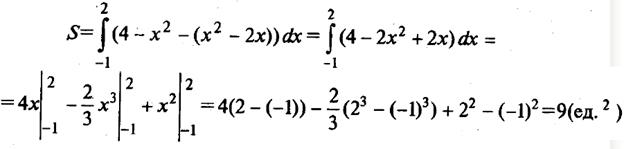
Пример 3. Найти площадь фигуры, ограниченной линиями у = 1/х;
y = х² и y = 4 в неотрицательной координатной четверти.

График функции у = 1/х представляет собой гиперболу, при положительных х она выпукла вниз; оси координат являются асимптотами. График функции у = х² в неотрицательной координатной четверти – ветвь параболы с точкой минимума в начале координат. Эти графики пересекаются при 1/х = х²; х³ = 1; х = 1; у = 1.

Прямую y = 4 график функции у = 1/х пересекает при х =1/4, а график функции у = х² при х = 2 (или -2).

Таким образом, фигуру, площадь которой необходимо найти, можно представить на рисунке 4.11.

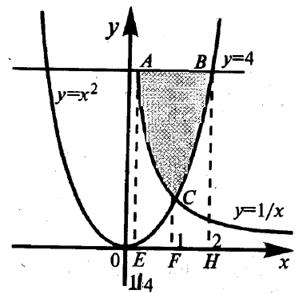
Рисунок 4.11 - Фигура, ограниченная линиями у = 1/х; y = х² и y = 4 в неотрицательной координатной четверти

Искомая площадь фигуры ABC равна разности между площадью прямоугольника АВНЕ, которая равна 4*(2 – ¼) = 7, и суммой площадей двух криволинейных трапеций АСFЕ и СВНF. Вычислим площадь АСFЕ:

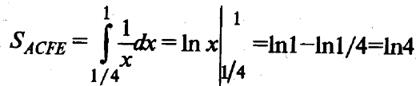
Вычислим площадь СВНF:

.

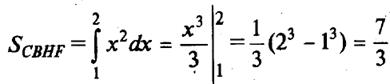Итак, искомая площадь равна 7 – (ln 4 + 7/3) = 14/3 – ln 4 » 3,28 (ед.²).