Свойства определенного интеграла. Приведем без доказательства некоторые важные свойства определенного интеграла.
Приведем без доказательства некоторые важные свойства определенного интеграла.
1. Постоянный множитель можно выносить за знак интеграла:
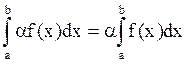 ,
,
где a - некоторое число.
2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых):

Отметим, что названные свойства определенного интеграла аналогичны свойствам неопределенного интеграла.
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b и с

4. Обе части неравенства можно почленно интегрировать, т.е. если на отрезке [а, b] ( а < b) f(x) £ g(x), то
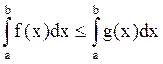
Следствие. Пусть на отрезке [а, b], где а < b, m £ f(x) £ M, где m и М - некоторые константы. Тогда 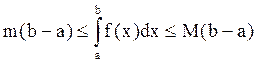 . Это вытекает из того, что
. Это вытекает из того, что 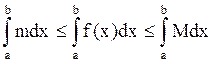 , а интегралы от констант вычисляются по формулам
, а интегралы от констант вычисляются по формулам 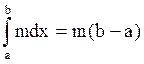 и
и 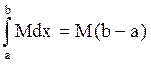 .
.
Т.е. если функция ограничена сверху и снизу некоторыми числами, то интеграл от этой функции ограничен произведениями этих чисел на длину отрезка (промежутка интегрирования).
5. Теорема о среднем. Если функция у = f(х) непрерывна на отрезке [а, b], где а < b, то найдется такое значение x Î [а, b], что  .
.
Геометрически теорема о среднем означает, что на отрезке найдется такая точка, что площадь под кривой у = f(х) на этом отрезке будет равна площади прямоугольника со сторонами у = f(x) и b – a (см. рисунок 4.5).
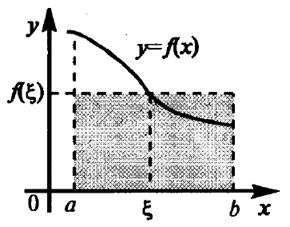
Рисунок 4.5 – Теорема о среднем
Интегралом с переменным верхним пределом называют функцию Ф(х) вида  , где x Î [а, b], а f(t) – функция, интегрируемая на отрезке [а, b].
, где x Î [а, b], а f(t) – функция, интегрируемая на отрезке [а, b].
Геометрический смысл интеграла с переменным верхним пределом представлен на рисунке 4.6 (этот интеграл равен площади S(x) под кривой
y =f(t) на отрезке [а, х]).
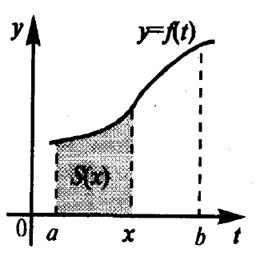
Рисунок 4.6 – Интеграл с переменным верхним пределом
Рассмотрим без доказательства свойства интеграла с переменным верхним пределом:
1. Если функция f(t) непрерывна на отрезке [а, b], то функция Ф(х) также непрерывна на [а, b].
2. Производная от интеграла с переменным верхним пределом по верхнему пределу равна подынтегральной функции:
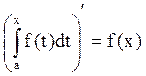
Дата добавления: 2015-10-06; просмотров: 1120;
