Несобственный интеграл

До сих пор при рассмотрении неопределенного интеграла мы рассматривали конечные пределы интегрирования, и те функции, от которых брали интегралы, были непрерывны на конечных отрезках интегрирования. Следовательно, эти функции были ограничены на этих отрезках (иначе невозможно было бы ввести понятие интегральной суммы).

Чтобы обобщить понятие интеграла на случаи, когда концы отрезка итегрирования стремятся к бесконечности, либо сама функция является не ограниченной, вводят понятие несобственного интеграла.

Рассмотрим вначале случай, когда функция ограничена, но имеют место бесконечные пределы интегрирования.

Несобственным интегралом от ограниченной функции y = f(х) на полуинтервале [а, +¥[ называется следующий предел: .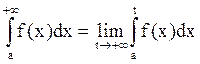

Если предел в правой части существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае - расходящимся.

Аналогично определяются несобственный интеграл на полуинтервале ]-¥; a] 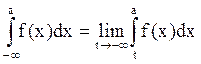и его сходимость.

Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры (см. примеры ниже).

Пример 1. Найти

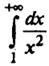
По определению

Тамким образом, заштрихованная на рисунке 4.12 площадь полубесконечной фигуры равна 1 ед².

Пример 2. Найти .

Найдем .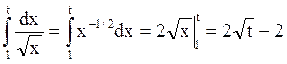

Тогда 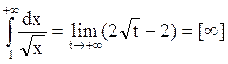. Этот несобственный интеграл является расходящимся, а соответствующая фигура имеет бесконечную площадь.

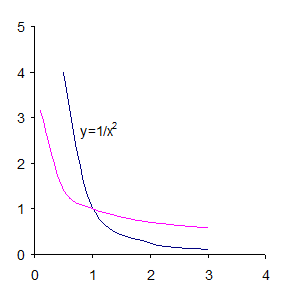
Рисунок 4.12 – Площади полубесконечных фигур (бесконечные пределы интегрирования)

Введем понятие несобственного интеграла на интервале ]-¥; +¥ [. Он представляет собой следующую сумму: 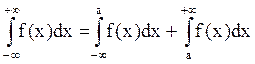(при условии, что каждое из слагаемых в правой части сходится). При этом интеграл называют сходящимся. Если хотя бы один из интегралов в правой части расходится, то и интеграл называется расходящимся.

Можно доказать, что введенное определение не зависит от выбора числа а.

Пример 3. Найти .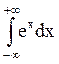

Исследуем на сходимость интегралы и 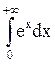(положим а = 0).

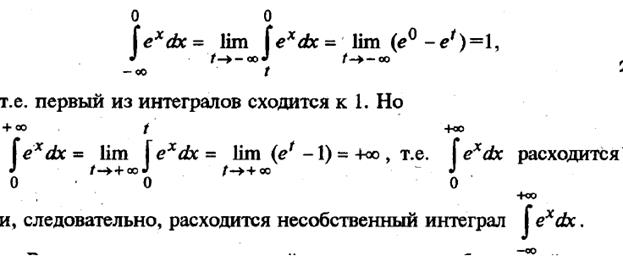
Теперь рассмотрим случай, когда функция непрерывна, но неограничена, а пределы интегрирования – конечны. Рассмотрим полуинтервал [а, b[.

Несобственным интегралом 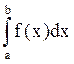от функции y = f(х) на полуинтервале [а, b[ называется предел 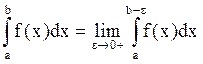, где e > 0.

Если предел в правой части существует и конечен, то несобственный интеграл называется сходящимся, в противном случае - расходящимся.

Аналогично вводится понятие несобственного интеграла от функции y = f(х), непрерывной, но неограниченной на ]a; b]: .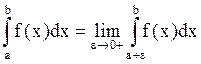

Пример 4. Найти .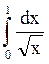

По определению .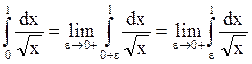

По формуле Ньютона—Лейбница .

Тогда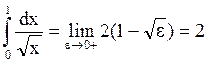

Следовательно, полубесконечная фигура (см. рисунок 4.13), ограниченная осями координат, кривой 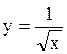и прямой х = 1, имеет конечную площадь, равную 2 ед².

y = 1 /

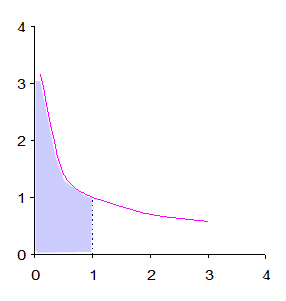
Рисунок 4.13 – Площадь полубесконечной фигуры (неограниченная функция)

Если функция f(x) не ограничена при х = с, где с Î [a; b], то интеграл 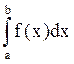также называют несобственным и определяют как 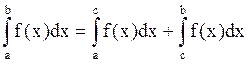(его считают сходящимся, если сходятся оба интеграла в правой части равенства, в противном случае он является расходящимся).

* (a + b)³ = a³ + 3a²b + 3b²a + b³