Вычисление интегралов вида
òsinm x cosn x dx(m и n – целые).
Если хоть одноиз mили nнечётное, то применима подстановка t = cos xили t = sin x.Причём интеграл сводится при этом к степенному интегралу. Основная идея: функции cosи sinберут от нечётной степени и подводят под знак дифференциала, выражая оставшееся через эту функцию.
Пример. òcos2 x sin3 x dx = òcos2 x sin2 x sin x dx = – òcos2 x sin2 x dcos x =
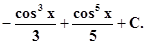
= –òcos2 x (1 – cos2 x) dcos x = –ò(cos2 x – cos4 x) dcos x =
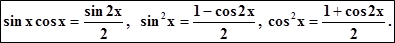 |
Если оба m и n чётные,то (как в 1)с)) применима подстановкаt = tg x .Однако, иногда удобно применять понижение степени с помощью формул:
Замечание.Интеграл вида òsinm x cosn x dxподстановкой t = sin2xили t = cos2xвсегда можно свести и к интегралу от биноминального дифференциала.
4. Интегрирование выражений, содержащих показательную функцию еx.
Рассмотрим несколько случаев:
а) I = òR(еx) dx –рационализирующей подстановкой является t = еx Þ x = ln t,
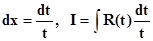
– интеграл от рациональной функции по t.
b)Интеграл вида I = òеax cos bx dxи I = òеax sin bx dxберутся по частям способом приведения t к самому себе. I = òеax cos bx dx, I = òеax sin bx dx

 u = cos bx u = sin bx
u = cos bx u = sin bx
dd = еax dx dd = еax dx
c)Интегралы вида òP(x) еax sin bx dxи òP(x) еax cos bx dxсводятся, очевдно, к интегралам видаòxm еax sin bx dxи òxm еax cos bx dx.Они вычисляются по частям понижением степени x.
 u = xm du = mxm–1dx
u = xm du = mxm–1dx
dd = еax cos bx dxи т. д.
Доходим до x0и вычисляем интеграл как раньше в b).
Дата добавления: 2015-10-05; просмотров: 1148;
