Вычисление вероятности в случае закона больших

При изучении теории вероятностей приходится использовать понятия случайного события и случайной величины. При этом предсказать заранее результат испытания, в котором может появиться или не появиться то или иное событие или какое-либо определённое значение случайной величины, невозможно, так как исход испытания зависит от многих случайных причин, не поддающихся учёту.

Однако при неоднократном повторении испытаний могут наблюдаться определённые закономерности. Эти закономерности, свойственные массовым случайным явлениям, и изучает теория вероятностей. Следует отметить, что математические законы теории вероятностей получены в результате абстрагирования реальных ситуаций, в которых наблюдаются случайные массовые явления.

При изучении результатов наблюдений над реальными случайными массовыми явлениями также имеют место некоторые закономерности. Следует обратить внимание на то, что они обладают свойствами устойчивости. Суть этого свойства состоит в том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин, наблюдаемых в испытаниях, при неограниченном увеличении числа испытаний становятся практически не случайными.

Предельные теоремы вероятностей устанавливают зависимость между случайностью и необходимостью. По смыслу их можно разбить на две группы, одна из которых называется законом больших чисел, а другая - центральной предельной теоремой.

Под законом больших чисел не следует понимать какой-то один общий закон, связанный с большими числами. Закон больших чисел - это обобщённое название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний средние величины стремятся к некоторым постоянным.

К этим теоремам относятся, теорема Чебышева и теорема Бернулли. Теорема Чебышева является наиболее общим законом больших чисел, а теорема Бернулли - простейшим.

Рассмотрим неравенство Чебышева. Оно справедливо для дискретных и непрерывных случайных величин. Рассмотрим дискретную случайную величину, заданную законом распределения:

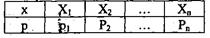
Оценим вероятность того, что отклонение случайной величины X от её математического ожидания не превышает по абсолютной величине числа 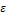. Если это число достаточно мало, то оценим вероятность того, что X принимает значение достаточно близкое к своему математическому ожиданию.

Неравенство Чебышева: вероятность того, что отклонение случайной величины X от её математического ожидания по абсолютной величине меньше положительного числа е не меньше чем разность 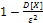, т.е.

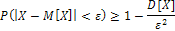
Замечание: Неравенство Чебышева даёт грубую оценку. Тем не менее, неравенство Чебышева имеет большое теоретическое значение. С его помощью доказываются теоремы и делаются теоретические выводы.

Теорема Чебышева: Если 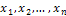- попарно независимые случайные величины и дисперсии их не превышают постоянного числа 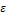, то каково бы ни было малое положительное число 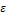. Вероятность неравенства

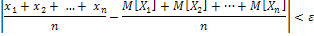
будет как угодно близка к 1, при условии, что число случайных величин достаточно велико. По-другому данное выражение можно записать

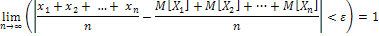
Теорема Бернулли: Если в каждом из 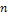независимых испытаний вероятность 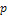- появления события А постоянна, то, как угодно близка к 1 вероятность того, что отклонение относительной частоты от вероятности 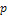по абсолютной величине будет сколь угодно малым, если .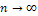

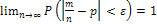Замечание: Теорема Бернулли утверждает, что при 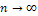относительная частота стремится к самой вероятности.