Числовые характеристики и медиана непрерывной случайной величины
Непрерывная случайная величина принимает сплошь все значения из некоторого промежутка, конечного или бесконечного. Закон распределения задается либо интегральной функцией распределения F(x), либо дифференциальной функцией  .
.
Эти функции связаны между собой:
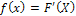
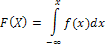
Вероятностный смысл F(x) - это вероятность того, что случайная величина X будет принимать значения меньше, чем х: 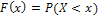 , например
, например 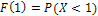 .
.
Вероятностный смысл f(x) - плотность распределения вероятности случайной величины X.
Свойства функции  :
:
а) непрерывная, неубывающая функция;
б)  ;
;
Свойства функции  :
:
а) 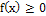 ;
;
б) 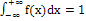 .
.
Вероятность попадания непрерывной случайной величины X в заданный промежуток 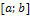 можно найти по формулам:
можно найти по формулам:
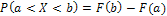
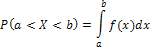
Основные числовые характеристики непрерывной случайной величины:
1. Математическое ожидание: 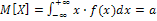 .
.
2. Дисперсия: 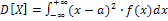 .
.
Второй способ вычисления дисперсии:
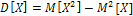 , где
, где
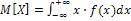 ;
; 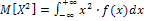
3. Среднее квадратическое отклонение: 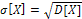 .
.
Начальный теоретический момент порядка к непрерывной случайной величины X определяется равенством 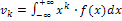 .
.
Центральный теоретический момент порядка к непрерывной случайной величины X определяется равенством 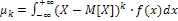 . В частности, если все возможные значения X принадлежат интервалу, то
. В частности, если все возможные значения X принадлежат интервалу, то 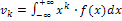 ,
, 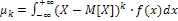 . Очевидно, что если
. Очевидно, что если 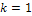 , то
, то 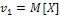 ,
,  ; если
; если  , то
, то 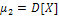 .
.
Центральные моменты выражаются через начальные моменты по формулам:
 .
.
Дата добавления: 2015-09-25; просмотров: 1909;
