Примеры. Задача 1. Найти математическое ожидание случайной величины , если известны математические ожидания и .
Задача 1. Найти математическое ожидание случайной величины 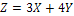 , если известны математические ожидания
, если известны математические ожидания 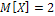 и
и 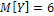 .
.
Решение: Используя свойства математического ожидания (математическое ожидание суммы равно сумме математических ожиданий слагаемых; постоянный множитель можно вынести за знак математического ожидания), получим
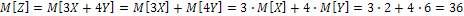
Задача 2. Найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины X по данному закону ее распределения, заданному таблично:

Решение. Заметим, что 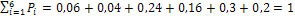 .
.
а) математическое ожидание:
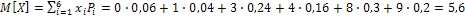 .
.
б) дисперсию случайной величины найдем двумя способами:
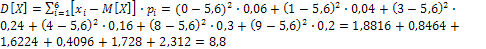 .
.
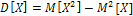 .
.
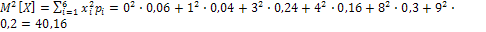 .
.
Тогда 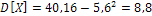 .
.
в) среднее квадратичное отклонение:
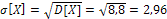 .
.
Ответ: а) 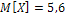 ; б)
; б) 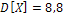 ; в)
; в) 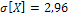 .
.
Дата добавления: 2015-09-25; просмотров: 3706;
