Вычисление интегральной функции распределения нормально распределенной величины
Функцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина X примет значение, меньшее х, то есть 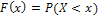 .
.
Часто вместо термина «функция распределения» используют «интегральная функция распределения».
Функция распределения обладает следующими свойствами:
1. Значения функции распределения принадлежат отрезку [0;l]: 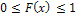 .
.
2. Функция распределения есть неубывающая функция: 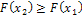 , если
, если 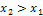 .
.
Следствие 1: Вероятность того, что случайная величина X примет значение, заключенное в интервале 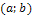 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 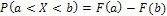 .
.
Следствие 2: Вероятность того, что непрерывная случайная величина X примет одно определенное значение, например 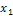 , равна нулю:
, равна нулю: 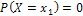 .
.
Если все возможные значения случайной величины X принадлежит интервалу 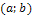 , то
, то 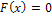 при
при 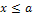 ;
; 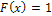 при
при 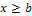 .
.
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: 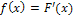 .
.
Часто вместо термина «плотность распределения» используют термины «плотность вероятностей» и «дифференциальная функция».
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a; b), определяется равенством
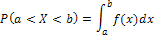
Зная плотность распределения, можно найти функцию распределения
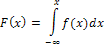
Плотность распределения обладает следующими свойствами:
1. Плотность распределения неотрицательна, то есть 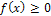 .
.
2. Несобственный интеграл от плотности распределения в пределах от 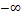 до
до  равен единице:
равен единице: 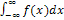 .
.
В частности, если все возможные значения случайной величины принадлежат интервалу 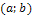 , то
, то 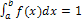 .
.
Дата добавления: 2015-09-25; просмотров: 2309;
