Примеры. Задача 1. Устройство состоит из 10 независимо работающих элементов
Задача 1. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется: а) меньше двух; б) не меньше двух.
Решение: а) Обозначим через X дискретную случайную величину - число отказавших элементов за время Т. Тогда 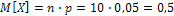 ;
; 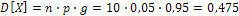 . Воспользуемся неравенством Чебышева:
. Воспользуемся неравенством Чебышева:
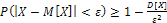 . Подставив сюда
. Подставив сюда 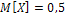 ,
, 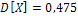 ,
, 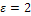 , получим
, получим 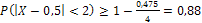
б) События 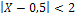 и
и 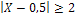 противоположны, поэтому сумма их
противоположны, поэтому сумма их 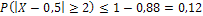 .
.
Ответ: а) 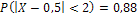 ; б)
; б) 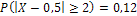 .
.
Задача 2. Вероятность появления события 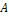 в каждом испытании равна
в каждом испытании равна  . Используя неравенство Чебышева, оценить вероятность того, что число
. Используя неравенство Чебышева, оценить вероятность того, что число 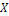 появлений события
появлений события 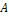 заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.
заключено в пределах от 40 до 60, если будет произведено 100 независимых испытаний.
Решение: Найдем математическое ожидание и дисперсию дискретной случайной величины 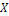 - числа появлений события
- числа появлений события 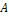 в 100 независимых испытаниях:
в 100 независимых испытаниях: 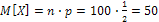 ;
; 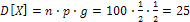 .
.
Найдем максимальную разность между заданным числом появлений и математическим ожиданием 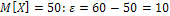 .
.
Воспользуемся неравенством Чебышева в форме 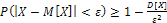 . Подставляя
. Подставляя 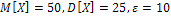 , получим
, получим 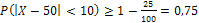 .
.
Ответ:  .
.
Дата добавления: 2015-09-25; просмотров: 6481;
