Построение по заданной выборке ее статистического ряда, полигона частот и частостей

Пусть для изучения количественного (дискретного или непрерывного) признака X из генеральной совокупности извлечена выборка 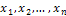объема 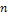. Наблюдавшиеся значения 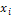, признака X называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом.

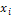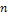Статистическим распределение выборки называют перечень вариант , вариационного ряда и соответствующих им частот , (сумма всех частот равна объему выборки ) или относительных частот 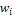(сумма всех относительных частот равна единице).

Статистическое распределение выборки можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал).

Дискретное распределение признака X

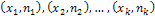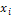Полигоном частот называют ломаную линию, отрезки, которой соединяют точки , где - варианты выборки и - соответствующие им частоты.

Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки 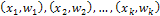, где 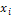- варианты выборки и 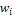- соответствующие им относительные частоты.

Непрерывное распределение признака X

При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины 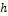и находят - сумму частот вариант, попавших в 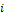- интервал. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 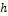, а высоты равны отношению 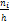(плотность частоты). Площадь частичного -го прямоугольника равна – сумме частот вариант, попавших в 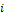- интервал. Площадь гистограммы частот равна сумме всех частот, то есть объему выборки .

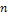Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 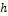, а высоты равны отношению (плотность относительной частоты). Площадь частичного -го прямоугольника равна 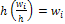- относительной частоте вариант, попавших в 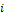- интервал. Площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.