Выполнение операций над графами. Построение матриц смежности, инциденций и достижимости для ориентированных графов
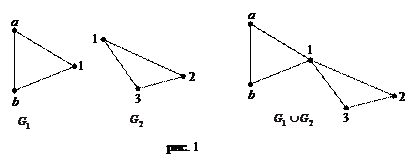 Объединением двух, или более графов называется граф, у которого множество вершин и множество дуг объединены (рис. 1).
Объединением двух, или более графов называется граф, у которого множество вершин и множество дуг объединены (рис. 1).
Суммой графов 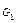 и
и 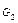 называется граф, определяемый как объединение графов, причем каждая вершина, не вошедшая в объединение, соединяется с другими вершинами (рис. 2).
называется граф, определяемый как объединение графов, причем каждая вершина, не вошедшая в объединение, соединяется с другими вершинами (рис. 2).
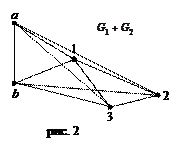 Произведением двух графов называется граф, каждая вершина которого представляет собой бинарное отношение (рис. 3).
Произведением двух графов называется граф, каждая вершина которого представляет собой бинарное отношение (рис. 3).
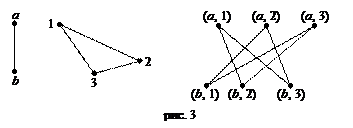 |
Матрицей смежности ребер графа называется такая матрица 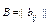 , что
, что 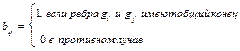 .
.
Пусть  - дуги, а
- дуги, а 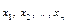 - вершины ориентированного графа
- вершины ориентированного графа 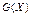 .
.
Матрица 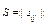 , такая что
, такая что 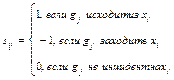 называется матрицей инциденций для дуг графа.
называется матрицей инциденций для дуг графа.
Матрица 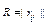 размером
размером 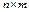 , где
, где 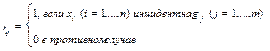 называется матрицей инциденций для ребер графа.
называется матрицей инциденций для ребер графа.
Пример
Для графа изображенного на рисунке 4 найти: 1) матрицу смежности (вершин); 2) матрицу инциденций; 3) матрицу отклонений; 4) вектор отклоненностей; 5) радиус, диаметр, центр и периферийные вершины.
В качестве примера рассмотрим схему первой (1870г.) сети связи для почтовых голубей (рис. 4).
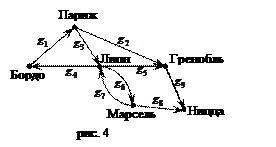 Для построенного графа найдем:
Для построенного графа найдем:
1. матрицу смежности (вершин)
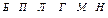
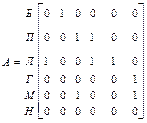
2. матрицу инциденций для дуг и для ребер
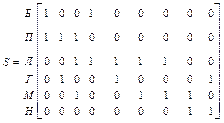
3. матрицу отклонений
| Города | П | Б | Л | Г | М | Н |
| Париж | ||||||
| Бордо | ||||||
| Лион | ||||||
| Гренобль | ∞ | ∞ | ∞ | ∞ | ∞ | |
| Марсель | ||||||
| Ницца | ∞ | ∞ | ∞ | ∞ | ∞ |
4. вектор отклоненностей
| Города | П | Б | Л | Г | М | Н |
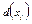
| ∞ | ∞ |
5. радиус, диаметр, центр, периферийные вершины
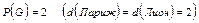
диаметр: ∞
центр: 2 (Париж, Лион)
периферийные вершины: Гренобль, Ницца.
Дата добавления: 2015-09-25; просмотров: 2234;
