Интегрирование выражений вида R(sin x, cos x)
Сразу заметим, что функция R(sin x, cos x)может содержать и tg x, ctg x, sec x, cosec x,т. к. они рационально выражаются через sin x иcos x.
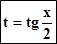 Интегралы òR(sin x, cos x) dxвсегда вычисляются в конечном виде через элементарные.
Интегралы òR(sin x, cos x) dxвсегда вычисляются в конечном виде через элементарные.
Универсальной рационализируещей подстановкойздесь является
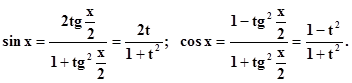 – p < x < p.
– p < x < p.
В самом деле
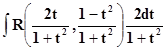
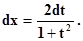
x = 2 arctg t,Тогда òR(sin x, cos x) dx = –
интеграл от рациональной функции по t.
Особенно употребительна универсальная тригонометрическая подстановка в
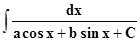
интегралах вида
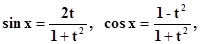
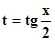
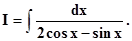
Пример.Полагают ,
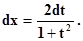
x = 2arctg t ,
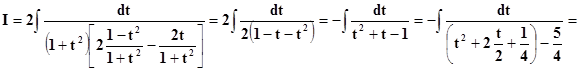 Тогда
Тогда
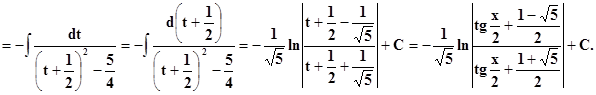 |
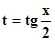
Подстановка является универсальной для интегралов òR(sin x, cos x)dx,но практическое применение её в ряде случаев приводит к громоздким вычислениям. Поэтому в некоторых частных случаях интегрирование проводят с помощью более простых подстановок.
a)Если функция R(sin x, cos x)изменяет знак при изменении знакаsin xна– sin x,то применяют подстановкуt = cos x
Действительно, если R(– sin x, cos x) = – R(sin x, cos x)имеет видR(sin x, cos x) = R1(sin2 x, cos x)sin xи ò R(sin x, cos x) dx = òR1(sin2 x, cos x)sin x dx =
= –òR1(1 – cos2 x, cos x)d cos x = –òR1(1 – t2, t) dt→ интеграл от рациональной функции по t.
b)Совершенно аналогично, если R(sin x, – cos x) = – R(sin x, cos x),то применяется подстановка t = sin x .В этом случае R(sin x, cos x) = R2 (sin x,
cos2 x)cos xи òR(sin x, cos x) dx = R2(sin x, cos2 x)cos x dx = òR2(t, 1 – t2) dt→ интеграл от рациональной функции по t.
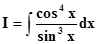
Пример.изменяем на противоположный знак при изменении знака sin x. t = cos x
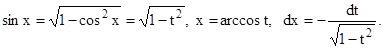
– 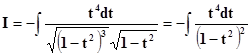 пришли к интегралу от рациональной дроби.
пришли к интегралу от рациональной дроби.
Интегрируя её и заменяя в конечном результате t = cos x,вычислим исходный интеграл.
c)Если функция R(sin x, cos x)не изменяет знака при одновременной замене знаков и sin xиcos x,то применим подстановку t = tg x(это в частности, когда sin иcosвходят только в чётных степенях)
Действительно, т. к. R(– sin x, – cos x) = R(sin x, cos x),то можно записать
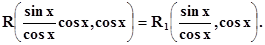
R(sin x, cos x) =НоR1 = Rи поэтому не
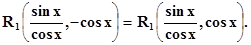
изменяет знака, т. е. А это может быть, если
cos xна самом деле входит лишь в чётных степенях, т. е.
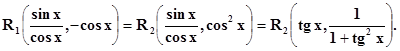
Но тогда
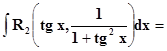
òR(sin x, cos x) dx =
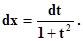
Применяем t = tg x, x = arctg t,
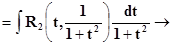
интеграл от рациональной функции.
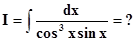
Пример.Знак не меняется при одновременной замене.
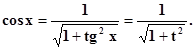
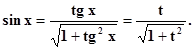
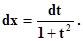
t = tg x, x = arctg t,

Дата добавления: 2015-10-05; просмотров: 6201;
