Интегрирование выражений вида R (x, ). Подстановки Эйлера.
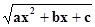
Выражение R (x, ),оноявляется рациональной
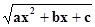 функцией от xи
функцией от xи
a, b, c –действительные числа, называют иногда функцией с квадратичной иррациональностью.Оказывается, всякий неопределённый интеграл вида
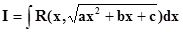
может быть вычеслен в конечном виде. Будем в дальнейшем
предпологать, что квадратный трёхчлен ax2 + bx + cне имеет равных действительных корней, так как в этом случае подинтегральное выражение сразу есть рациональная функция (т. к. корень заменяется рациональным выражением). Изучим три подстановки Эйлера, с помощью которых всегда можно рационализировать подинтегральное
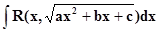
выражение, т. е. (1) свести к интегралу от рациональной функции.
I) Первая подстановка Эйлераприменяется, если a > 0.Тогда полагают
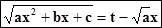
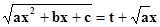
(можно и ).
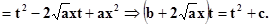
Возведём это равенство в квадрат: ax2 + bx + c
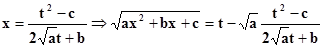
– рациональное выражение от t.
Но тогда и dx будет рационально выражаться через t (самим найти dx).
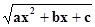
Т. к. x, , dxрационально выражается через t, то интеграл (1) действительно сводится к интегралу от рациональной функции по t.Интегрируя и
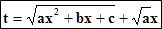
заменяя в результате t через x ,вычисляем интеграл.

Пример. a = 1 > 0. D = b2 – 4ac = 1 – 4 = – 3 < 0
–действительных корней нет.
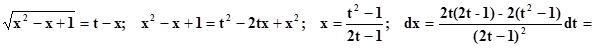
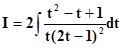
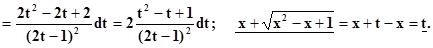 |
Итак – интегрируем как рациональною дробь и в результате

заменяем (самостоятельно).
II) Вторая подстановка Эйлераприменяется, если c > 0.Тогда полагают
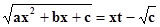
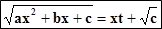
(можно было бы )
Возводя равенство в квадрат, уничтожая св обеих частях, сокращая на x,получим уравнение первой степени относительно x. Из чего найдём x, как рациональную функцию от t. Тогда и dx есть рациональная функция от t, а потому и исходный интеграл I рационализируется.
Практически случай II легко сводится к случаю I, если a < 0, c > 0. Достаточно использовать замену переменной x = 1/z.Тогда в новом подинтегральном выражении c станет играть роль а, и можно применить I подстановку Эйлера.
Таким образом, пользование второй подстановкой Эйлера всегда можно избежать, хотя она бывает и удобна.

Пример.Вычислить с помощью второй подстановки
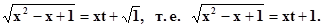 |
Эйлера (самостоятельно)
III) Третья подстановка Эйлераприменяется в тех случаях, когда квадратный трёхчлен ax2 + bx + cимеет различные вещественные корни:αиβ.
Тогда он разлагается в произведение ax2 + bx + c = а(x – α)(x – β).
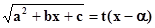
В этом случае применяется подстановка ,
 можно и
можно и
Возведём в квадрат a2 + bx + c = t2(x – α)2 Þ a(x – α)(x – β) = t2(x – α)2 Þ ax – βa = xt2 – αt2.
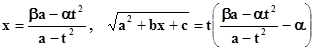
– рациональная функция.
Т. к. x рациональная функция, то и dx тоже рациональная функция от t. Но тогда интеграл (1) действительно преобразуется в интеграл от 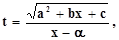 рациональной функции по переменной t.
рациональной функции по переменной t.
Вычисляя этот интеграл и заменяя в результате t через x,
вычислим интеграл I в конечном виде.
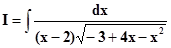
Пример. 1и 2подстановки не применимы
– 3 + 4x – x2 = – 1(x – 3)(x – 1)
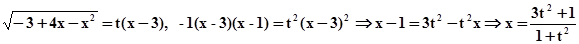 |

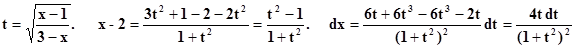 |
Теперь имеем:
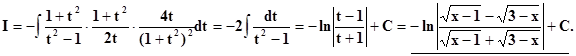
Замечание.Можно показать, что I) и III) подстановки Эйлера одних достаточно, чтобы рационализировать подинтегральное выражение I в любых случаях. В самом деле, если ax2 + bx + cимеет вещественные корни, то применима вторая подстановка. Если действительных корней нет, то D = b2 – 4ac < 0.Преобразуем трёхчлен так:
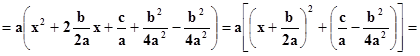
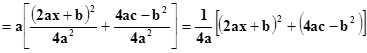 |
ax2 + bx + c
Видно, что знак трёхчлена совпадает со знаком a.
Если a > 0,то применим I)подстановку.
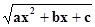 Если же a < 0,то ax2 + bx + c < 0и поэтому вообще не существует.
Если же a < 0,то ax2 + bx + c < 0и поэтому вообще не существует.
Таким образом, Iи IIподстановки Эйлера позволяют свести указанный интеграл в любом случае к интегралу от рациональной функции, а значит и вычислить его в конечном виде.
Теоритическая ценность подстановок Эйлера очевидна. Однако на практике пользование ими приводит к громоздким вычислениям. Поэтому стараются по возможности в более простых интегралах применять и другие методы.
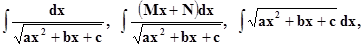
Так, например, интегралы вида:
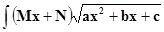
удобнее вычислять выделением полного квадрата и
последующей заменой переменной.
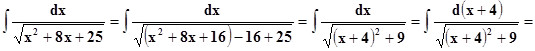
Дата добавления: 2015-10-05; просмотров: 3702;
