Блок-схема метода Эйлера.

Задаются начальные значения 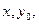величина шага 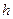и количество

расчетных точек 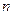, как показано на рисунке 17.1. Решение получается в узлах 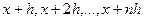. Вывод результатов предусмотрен на каждом шаге.

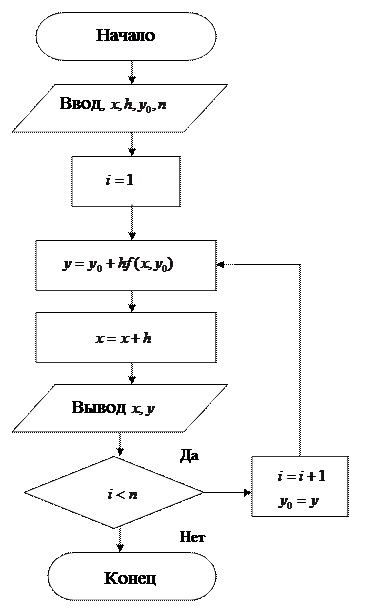
Рисунок 17.1 Блок-схема метода Эйлера.

Краевая задача.

Понятие решения краевой задачи.

Если при решении обыкновенных дифференциальных уравнений

задаются условия для двух значений независимой переменной (на концах рассматриваемого отрезка), то такие задачи называются краевыми.

Рассмотрим линейное дифференциальное уравнение второго порядка:

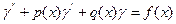. (17.1)

Краевая задача состоит в отыскании решения 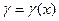уравнения (17.1) на отрезке [а,b], удовлетворяющего на концах отрезка условиям

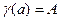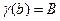; . (17.2)

Граничные условия могут быть заданы не только в частном виде (17.2), но и в общем:

,

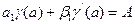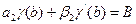. (17.3)

Методы решения краевых задач могут быть:

точные аналитические, приближенные и численные.