Аппроксимация производных.

Как известно производной функции 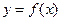называется предел отношения приращения функции 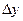к приращению аргумента 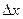при стремлении его к нулю:

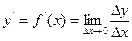. (15.1)

В численных расчетах на ЭВМ для вычисления производных используют приближенное равенство:

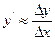(15.2).

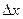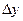При этом и полагают равным некоторому конечному числу. Поэтому это соотношение (14.2) называется аппроксимацией производных с помощью отношения конечных разностей.

Для функции 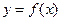, заданной в табличной форме в виде: 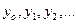и 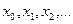предположим, что разность между соседними значениями аргумента постоянна и равна шагу 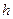. Выражения для вычисления производно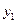й при 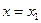в зависимости от способа нахождения конечных разностей могут быть следующими:

способ левых разностей

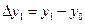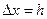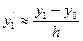; ; ; (15.3)

способ правых разностей

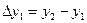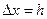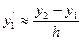; ; ; (15.4)

способ центральных разностей

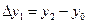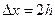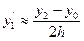; ; ; (15.5).

Используя этот прием можно найти приближенные значения производных любого порядка.

Решение обыкновенных дифференциальных уравнений численными методами.

Понятие решения обыкновенных дифференциальных уравнений (ОДУ).

Многие задачи механики, физики и других отраслей науки и техники

при их математическом моделировании сводятся к дифференциальным уравнениям. В зависимости от числа независимых переменных дифференциальные уравнения делятся на обыкновенные, содержащие одну независимую переменную, и уравнения с частными производными, содержащие несколько независимых переменных.

Будем рассматривать обыкновенные дифференциальные уравнения, которые в общем виде записываются:

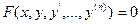, (15.6)

где 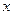- независимая переменная,

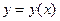- линейная функция,

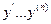- производные от первого до 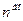порядка.

Решением дифференциального уравнения (15.5) называется всякая функция 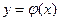, которая после ее подстановки в уравнение превращает его в тождество. Общее решение дифференциального уравнения 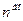порядка:

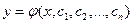, (15.7)

где 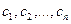-произвольные постоянные.

Геометрически общее решение ОДУ описывается бесконечным семейством интегральных кривых с параметром 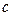, а частному решению соответствует одна кривая с параметром 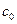. Для выделения частного решения уравнения первого порядка достаточно задать координаты 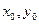произвольной точки, т.е. одно дополнительное условие.

Для решения уравнений более высокого порядка надо задать столько дополнительных условий, сколько произвольных постоянных в общем решении, т.е. каков порядок уравнения.

В зависимости от способа задания дополнительных условий для получения частного решения ОДУ выделяют два типа задач:

1. Задачи Коши соответствуют заданию условий в одной точке 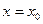, которая

называется начальная точка начального условия.

2. Краевые задачи соответствуют заданию условий в более, чем одной точке,

например, в двух точках 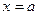и 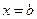. Условия называются граничными или краевыми.