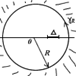
Аппроксимация Паде и ортогональные многочлены.

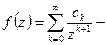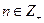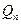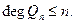Рассмотрим ряд произвольный. Зафиксируем и рассмотрим Р-задачу: будем искать многочлен со свойствами: 1) 2) 3) 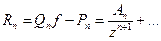для некоторого многочлена 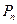ряд начинается со степени

Замечание. Решение этой задачи существует, т.к. система 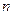линейных уравнений однородна относительно 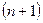неизвестных коэффициентов многочлена .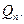

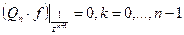Замечание (о единственности). С точностью до нормировки такой единственности нет (возьмём ).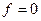

Но при этом:

Задача. Отношение многочленов определяет единственную рациональную дробь, заметим, что 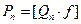- многочлен 2 рода, а ряд 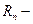называется функцией 2 рода.

Определение. Дробь 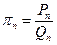называется аппроксимацией Паде ряда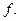

Замечание. Если для любого решения Р-задачи, многочлен 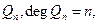то 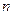нормалбный индекс и единственно (с точностью до нормировки).

Если функция Марковского типа, то многочлен 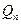удовлетворяет следующим соотношениям ортогональности: 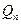называется ортогональным многочленом.

Доказательство. Посчитаем этот интеграл 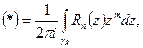применяя основную

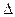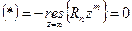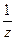
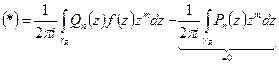теорему о вычетах к области вне круга (окружность проводим так, чтобы было внутри): - т.к. отсутствует . С другой стороны: как интеграл по замкнутому контуру ИТК. Изменим порядок интегрирования по теореме Фубини интеграл Коши (формула Коши для Круга)

Утверждение. Если 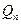ортогональный многочлен, то 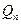имеет 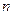простых нулей внутри отрезка .

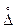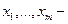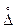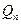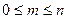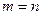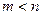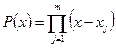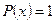Доказательство. Обозначим все различные точки внутри отрезка , в которых многочлен меняет знак (нули нечётной кратности). Хотим доказать, что . От противного. Пусть . Рассмотрим следующий многочлен: , если то . на 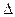(не меняет знак). Она равняется 0 в конечном числе точек. Она > 0 на множестве положительной 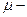меры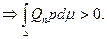

В силу соотношения ортогональности: 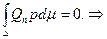противоречие.

Следствие. Если 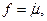то все индексы 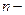нормальны. (с точностью до нормировки). Для определённости 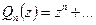- старший коэффициент = 1.

Свойства таких многочленов:

Утверждение. Ортогональные многочлены удовлетворяют рекуррентному соотношению: 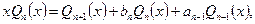где 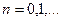. При этом выполняются начальные условия: 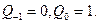При этом 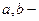некоторые коэффициенты.

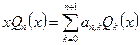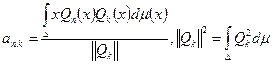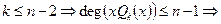
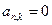
Доказательство. Возьмём - разложили по базису. Это ортогональная система в . Коэффициенты вычисляются по формулам Фурье: . Пусть Остались 3 слагаемых: 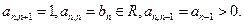Почему? Воспользуемся той же формулой: 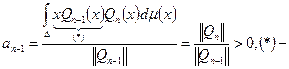многочлен степени 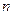со старшим коэффициентом 1, т.е. 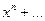, заменяем его на .

!!!

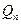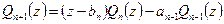Утверждение. Многочлены 2ого рода удовлетворяют такому же рекурсивному соотношению: 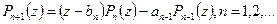, при этом выполняютя начальные условия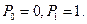

Доказательство. 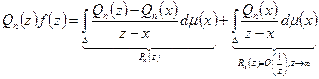. Рассмотрим: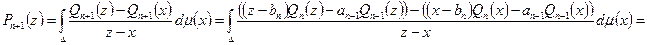

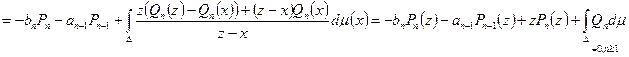
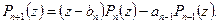
Вывод (следствие). Аппроксимация Паде 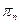суть подходящие дроби для непрерывной дроби: 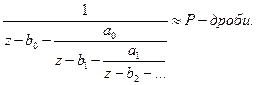Таким образом сходимость дроби к функции можно заменить на сходимость аппроксимации к функции.