Аппроксимация экспериментальных данных
Аппроксимацией называется подбор аналитической формулы у = f(x) для установленной из опыта функциональной зависимости 
Аппроксимируемая функция у может зависеть от одной или от нескольких переменных. Рассмотрим оба случая.
Одна независимая переменная. В простейшем случае задача аппроксимации для функции одной переменной выглядит следующим образом.
Пусть имеются данные, полученные в ходе эксперимента или наблюдений, которые можно представить в виде таблицы значений (х, у).
| х | 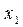
| 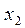
| … | 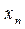
|
| у | 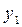
| 
| … | 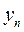
|
На основе этих данных требуется подобрать такую функцию у=f(x), которая с точки зрения некоторого критерия оптимальности наилучшим образом описывала бы экспериментальную зависимость.
Обычно задача аппроксимации распадается на две части. Сначала устанавливают вид зависимости у=f(x) и, соответственно, вид эмпирической формулы, то есть решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой. После этого определяются численные значения неизвестных параметров выбранной эмпирической формулы, для которых приближение к заданной функции оказывается наилучшим.
Для сглаживания экспериментальных зависимостей  , заданных таблично, в MS Excel [11,39,40] используются различные функции у = f(x):
, заданных таблично, в MS Excel [11,39,40] используются различные функции у = f(x):
- линейная;
- полиномиальная;
- логарифмическая;
- степенная;
- экспоненциальная.
Параметры аппроксимирующей функции подбираются так, чтобы выполнялось условие минимума среднеквадратичных отклонений (критерий оптимальности):

где 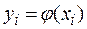 - экспериментальные точки (i= 1...n).
- экспериментальные точки (i= 1...n).
Степень точности аппроксимации экспериментальных данных в MS Excel оценивается коэффициентом детерминации (R2). Чем ближе этот коэффициент к значению 1, тем точнее приближение. При правильном выполнении процедуры аппроксимации полученная аналитическая зависимость позволяет вычислять значения функции в дополнительных точках. Для этого в ячейку листа MS Excel необходимо занести полученную в результате аппроксимации формулу со ссылкой на ячейку с независимой переменной.
В тех случаях, когда аппроксимируемая переменная у зависит от нескольких независимых переменных

используются следующие специальные функции Excel:
- ЛИНЕЙН и ТЕНДЕНЦ для аппроксимации линейных функций вида 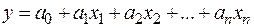 ;
;
-ЛГРФПРИБЛ и РОСТ для аппроксимации показательных функций вида 
Функции ЛИНЕЙН и ЛГРФПРИБЛ имеют одинаковые параметры:
· множество наблюдаемых значений у;
· множество наблюдаемых значений 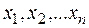 ;
;
· логическое значение, которое указывает, равна ли 0 константа а0;
· логическое значение (статистика), которое указывает, нужна ли дополнительная статистика по регрессии.
Функции ТЕНДЕНЦИЯ и РОСТ позволяют находить точки, лежащие на аппроксимирующих кривых 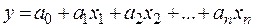 и
и 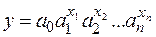 соответственно.
соответственно.
Обе функции имеют одинаковые аргументы:
- множество известных значений у;
- множество известных значений х;
- новые значения х (строка или столбец новых значений для каждой независимой переменной 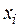 ;
;
-логическое значение для константы (равна нулю или нет).
Дата добавления: 2015-10-13; просмотров: 2360;
